Аналоговые оптические процессоры

Функциональная и структурная организации аналоговых оптических процессоров строится на основе функционально-целевого назначения. Когерентный аналоговый оптический процессор, использует методы пространственных преобразований с помощью масок, линз, волноводов и фильтров. Аналоговые оптические процессоры могут выполнять функции оптических корреляторов когерентного и некогерентного типов. Математические операции и задачи, реализуемые оптическим процессором, ограничены. Особенно эффективно использование методов голографии в задачах обработки информации. С помощью голографических устройств реализуют синтез пространственных операционных фильтров и преобразователей изображений.

Акустооптические процессоры корреляционного типа с пространственным и временным интегрированием используют для анализа быстропротекающих процессов. В частности они используются для анализа радиосигналов. Схема работы акустооптического спектроанализатора приведена на рис. 5.3.

Акустооптический спектроанализатор работает следующим образом. Когерентный пучок света 1 подают на пластину 3, в котором возбуждаются акустические волны частотой f ₁ пьезоэлектрическим преобразователем 2. Выходящий поl углом Брэгга луч фокусируется линзой Л в фокальной плоскости в точку а.

Рис. 5.3. Схема работы акустооптического спектрального

анализатора

Если частота акустической волны изменится на f ₂, то выходящий луч сфокусируется в точку б. Таким образом, если на пьезоэлектрический преобразователь подавать радиосигнал с изменяющейся или модулированной частотой, то в фокальной плоскости будет формироваться спектр сигнала. Обычно в фокальной плоскости размещают линейку фотодиодов или фотокамеру, позволяющую воспроизводить спектр сигнала в удобном для восприятия и анализа виде.

Применяют также акустооптические анализаторы спектра с пространственным и временным интегрированием. Более сложные акустооптические процессоры используют для обработки сигналов фазированных антенных решеток, используемых в радиолокации.

Если в пластине 3 (рис.5.3) возбуждать колебания одной частоты и подавать на неё белый свет, то в фокальной плоскости линзы получим равномерный спектр. Пропустив предварительно свет через кювету с жидкостью, мы получим спектры поглощения присутствующих в ней веществ. Таким образом, акустооптические анализаторы можно успешно применять для спектрального анализа.

Аналогично предыдущему случаю (рис.5.3) строится оптический процессор для двумерного преобразования Фурье.

Для этого используют монохроматический луч и прозрачный транспарант со штриховым изображением.

Плоский фронт когерентного пучка света, прошедший через транспарант (рис. 5.4), в линзе Л1 преобразуется в сферический, а пучок (луч) преобразуется в пространственный спектр в фокальной плоскости линзы. Лучи, направленные под углом к оси линзы фокусируются в фокальной плоскости со смещением. Таким образом, угловое распределение спектра за линзой преобразуется в пространственное распределение в фокальной плоскости. В фокальной плоскости линзы мы получим преобразование Фурье:

F { G(x,y) } =g(φ,ξ)=∫∫ G(x,y) exp[ -j(px+qy) ] dxdy, (5.11)

где постоянные и равны

Рис. 5.4. Прямое и обратное преобразование Фурье от

изображения

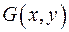– пространственное распределение света на транспаранте, 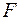– фокусное расстояние линзы; интегрирование ведется по площади транспаранта.

Восстановить изображение, можно используя обратное преобразование Фурье с помощью линзы Л2:

F { g(φ,ξ) } = G′(x,y)= (1/2π) ∫∫ g(φ,ξ) exp[ j(px+qy) ] dpdq, (5.12)

где G′(x,y) пространственное распределение света на экране, интегрирование ведется по угловому распределению g(φ,ξ) в фокальной плоскости линзы Л1.

Преобразование Фурье можно фильтровать масками. Диафрагменное отверстие обрезает высшие гармоники и смягчает резкие границы изображения. Маска, закрывающая центр фокуса делает резче границы и дает контрастное изображение.

В заключение необходимо отметить, что современные вычислительные машины находятся на пределе быстродействия, требуются и создаются вычислительные машины с параллельной обработкой информации. Оптические процессоры позволяют производить операции с двумерными массивами и изображениями. Кроме того они, в отличии от электрических цепей, не имеют ограничений по быстродействию, обусловленных индуктивностью и емкостью.

В настоящее время появилось новое направление электроники, функциональная электроника. Её использование связано с тем, что обработка быстропротекающих процессов в радиотехнике оказалась эффективной при одновременном использовании полей разной физической природы. Примером является акустооптический спектроанализатор, позволяющий обрабатывать радиосигналы с частотой до 1 ГГц.

Дата добавления: 2015-07-11