|
Читайте также: |
Поскольку оптические свойства молекул определяются поляризуемостью, магнитное вращение связано с влиянием магнитного поля на поляризуемость. Более точно можно сказать, что под влиянием магнитного поля появляются анизотропные компоненты тензора поляризуемости. Влияние магнитного поля можно выразить следующим образом:
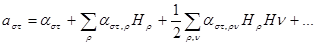
(7.2)
Здесь 
- координаты вектора напряженности магнитного поля. Тензор 
антисимметричен относительно перестановки первых двух индексов. Это можно показать следующим образом. Поскольку 
, где 
- вектор-потенциал, мы имеем:
(7.3)
Кроме того, из определения энергии как вещественной функции следует, что тензор 
- эрмитов, а величины 
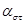должны быть минимальными. Рассмотрим феноменологически, как появляется оптическая анизотропия и вращение плоскости поляризации под действием магнитного поля. В случае анизотропной поляризуемости, возникающей под действием магнитного поля, соотношения между векторами 
и 
(поле 
направлено по оси) имеют вид:
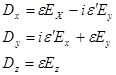(7.4)
В этом выражении величина 
, пропорциональна асимметричной мнимой компоненте поляризуемости 
(
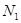-концентрация исследуемых молекул в единице объема). Рассмотрим также световую волну, распространяющуюся вдоль оси 
, которая имеет вид:
(7.5)
Уравнения (7.4) и (7.5) приводят к однородной системе уравнений:
(7.6)
Приравнивая определитель этой системы к нулю, получим: 
; 
; 
. При этом значение 
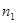соответствует соотношению 
, а 
, т.е. разным поляризациям световой волны. Поэтому разность хода для лево- и право циркулярно-поляризованных волн равна
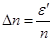(7.7)
В это случае на оптическом пути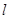 
плоскости поляризации
повернется на угол j, равный
(7.8).
Тогда, учитывая соотношение (7.7), получим следующее выражение для постоянной Верде: 
. Необходимо отметить, что согласно (7.2), e’~H.
Дата добавления: 2015-07-11; просмотров: 58 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Общая характеристика магнитного вращения. | | | Дисперсия магнитного вращения плоскости поляризации. |