Читайте также:
|
Формула (5.19) справедлива для отдельной пары донор-акцептор. В этом случае закон затухания флуоресценции донора после окончания возбуждения можно записать в виде:
(5.20)
где τD – время жизни флуоресценции донора без акцепторов, а km – константа скорости миграции энергии, определяемая согласно (5.14). В случае пространственного распределения доноров и акцепторов кинетические характеристики флуоресценци доноров несколько усложняются.
Рассмотрим случайное распределение доноров и акцепторов в однородной и изотропной среде. Предположим, что имеет место миграция энергии с доноров на акцепторы. Пусть концентрация возбуждённых доноров n(R,t), а невозбуждённых акцепторов N(R,t). Начало координат положим в месте нахождения молекулы донора.
Тогда изменения конгцентрации возбуждённых доноров и неводбуждённых акцепторов определяются уравнениями:
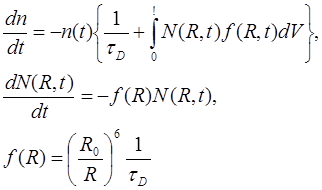(5.21
При t=0 (момент возбуждения доноров) N(R,0)=N0, n(0) = n0. Из этих уравнений следует, что конццентрация акцепторов в основном состоянии будет уменьшаться по закону:
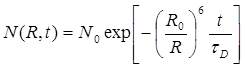(5.22)
В то же время концентрация возбуждённых доноров будет изменяться следующим образом:
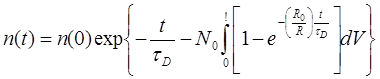(5.23)
Обозначим 
, тогда интесивность флуоресценции доноров будет
,
где
,
а C — некоторая постоянная. Приближённо можно считать, что 
.
Таким образом в случае хаотического распределения доноров и акцепторов при наличии миграции энергии закон затухания флуоресценции отличается от моноэкспонециального закона. Одноко, приведённое здесь рассмотрение не учитывает некоторых важных факторов, таких как дезактиващия акцепторов в процессе миграции энергии.
Дата добавления: 2015-07-11; просмотров: 97 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Индуктивно резонансный механизм; вывод формулы Ферстера; условия миграции. | | | Класификация Ферстера различных случаев миграции энергии. |