|
Читайте также: |
Из уравнений (4.1) и (4.2) в стационарном случае следует, что квантовый выход может быть выражен следующим образом:
(4.5)
Определим собственное (радиационное) время жизни как такое время жизни, которое имело бы люминесцирующее состояние, если бы отсутствовали все процессы дезактивации кроме флуоресценции. Таким образом, по определению
(4.6)
Тогда учитывая соотношения (4.3–4.6), получим
или 
(4.7)
Радиационное время жизни — это максимально возможное время жизни при φ = 1,т.е. при отсутствии всех процессов кроме флуоресценции. В реальном случае при наличии других процессов дезактивации τ и φ уменьшаются, оставаясь пропорциональными друг другу.
Радиационное время жизни связано с формой и интенсивностью спектров поглощения и флуоресценции. Предложено несколько формул для расчета радиационного времени жизни. Приведем некоторые из них. Одна из простейших формул, связывающих τr с 
, где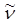 
— волновое число, имеет следующий вид:
(4.8)
Здесь 
означает волновое число, соответствующее линии зеркальной симметрии между спектрами флуоресценции и поглощения, построенными в шкале волновых чисел 
. Более сложная формула, учитывающая форму как полосы поглощения, так и спектра флуоресценции, имеет вид:
(4.9)
В этой формуле g0 и g1 — мультиплетности основного и возбужденного состояний соответственно, nf и na — средние показатели преломления растворителя в областях флуоресценции и поглощения, 
и 
- спектры флуоресценции и поглощения в шкале волновых чисел в мкм 
.
Формулу (4.8) можно упростить и получить следующее простое соотношение:
(4.10)
Для сильно поглощающих в видимой области красителей 
, поэтому 
с.
Получим теперь соотношение между квантовым выходом и константами скорости при наличии тушителя, т.е. в случае, когда, 
, q — концентрация тушителя в растворе. В этом случае уравнение (4.5) можно представить в виде:
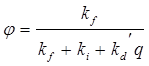(4.11)
Обозначим φ0 и τ0 — квантовый выход и время жизни флуоресценции без тушителя, т.е. при q=0, тогда
; 
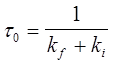
Таким образом, обратный квантовый выход флуоресценции прямо пропорционален концентрации тушителя (закон Штерна-Фольмера).
(4.12)
Дата добавления: 2015-07-11; просмотров: 92 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свойства спектров флуоресценции: правило Стокса, закон Вавилова, правило зеркальной симметрии В.Л. Левшина. | | | Флуоресценция и фосфоресценция. |