Дисперсия оптической активности в области аномальной дисперсии и круговой дихроизм.

Формулы для фактора вращения (6.5), а также формулы (6.6-6.9) не применимы в области собственного поглощения исследуемого вещества, т.е. в области аномальной дисперсии, так как знаменатель этих формул обращается в ноль. Для того, чтобы исправить положение, в рассмотрение вводят затухание, которое появляется в знаменателе дисперсионных формул. При этом формула для фактора вращения изменяется следующим образом:

(6.13)

Это полностью аналогично изменению формулы для поляризуемости в поглощающих средах:

(6.14)

где так называемая дипольная сила.

Введение комплексных величин и приводит к тому, что угол вращения плоскости поляризации линейно-поляризованного света и показатель преломления становится комплексными величинами

(6.15)

Величина (угол эллиптичности) характеризует разность в показателях поглощения право- и левоциркулярнополяризованного света. В этом случае аналогично (6.1) мы можем написать следующие соотношения:

(6.16)

В этой формуле показатель поглощения света, определяемой выражением:

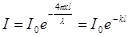(6.17)

Отделяя вещественные мнимые части в выражении (6.16), мы получим уже известные формулы

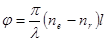; (6.18)

Сила вращения (6.13) связана с , также как дипольная сила в (6.14) связана с , а именно:

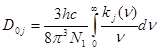; (6.19)

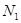В этих формулах - концентрация исследуемых молекул в единице объема; , 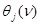показатели поглощения и эллиптичности в -полосе поглощения, обусловленной переходом на -энергетический уровень. Таким образом, в полосе поглощения молекулы не только происходит вращение плоскости поляризации линейно поляризованного света, но и имеет место превращение линейно-поляризованного света в элиптически поляризованный свет. Типичные зависимост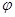и и в области аномальной дисперсии оптической активности и кругового дихроизма показаны на рис. 19

Рис. 19

Области аномальной дисперсии показаны пунктиром. Из теории измерений аномальной дисперсии оптической активности (АДОА) и кругового дихроизма следует, что чувствительность метода выше для кругового дихроизма, чем для АДОА.

Измерения в области полосы собственного поглощения дают ценную информацию о конформации биополимеров. Симметричные молекулы красителей, присоединенные к нативным белкам и нуклеиновым кислотам, приобретают свойства оптической активности и обнаружения АДОА КД в собственных полосах поглощения.

Таким образом были исследованы места расположения красителей, связанных с ДНК и моделирующих взаимодействия белков с нуклеиновыми кислотами.

Дата добавления: 2015-07-11