Положение спектра поглощения. Расчеты электронных уровней сложных молекул: одно- и много конфигурационное приближение.

Энергию электронного перехода можно рассчитать методами квантовой химии. Применим для этой цели уравнение Хартри-Фока. Они имеют вид:

(1.3)

Здесь - одноэлектронный гамильтониан остова, - одноэлектронная спин-орбитальная функция, Y_i - одноэлектронная энергия i-ой спин-орбитали.

Рассмотрим определение полной волновой функции молекулы в основном и возбужденных состояниях и соответствующих энергий, на примере системы с четырьмя электронами, в приближении замороженных орбиталей. Схема заполнения для основного состояния имеет вид:

Волновая функция основного состояния может быть записана следующим образом:

(1.4)

Энергия основного состояния равна:

(1.5)

Здесь 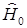- гамильтониан системы, а (интегрирование по координатам и суммирование по спинам всех электронов). Тогда

Возбужденные синглетные состояния описываются разностью двух детерминантов. Так, синглетное возбужденное состояние, возникающее при переходе электрона с обитали Y₁ на орбиталь Y₂ можно изобразить следующими схемами:

Волновая функция этого состояния может быть представлена в виде:

(1.6)

Энергия этого состояния может быть определена так:

(1.7)

Эта величина вычисляется с помощью правила вычисления матричных элементов от детерминантных функций. Величины e₁ и e₂ входят в уравнение Хартри-Фока и представляют собой орбитальные, одноэлектронные энергии.

Соответствующее триплетное состояние описывается тремя функциями, имеющими разные значения проекций спина (S_z =1,0,-1):

(1.8)

Энергия возбужденного триплетного состояния дается выражением:

(1.9)

В матричном элементе может стоять любая функция (1.8). Используя выражения (1.5) и (1.8), можно получить выражение для энергий переходов через орбитальные энергии, кулоновские и обменные интегралы.

(1.9)

Формула (1.10) получена в так называемом одно-конфигурационном приближении. Знак «+» соответствует синглету, а знак «-«триплету. Поскольку K₂₃ > 0, синглетный уровень лежит выше триплетного на величину 2K₂₃.

Более низкие энергии возбужденных состояний получаются в так называемом много конфигурационном приближении, когда волновая функция возбужденного состояния ищется в виде линейной комбинации функций вида (1.6). Обычно берут для линейной комбинации функции, отвечающие самым нижним возбужденным состояниям. Для примера рассмотрим волновую функцию, составленную из двух волновых функций:

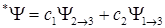
Функция Y_1®3 определяется аналогично функции (1.6). Коэффициенты C ₁ и C ₂ линейной комбинации (1.10) определяются из однородной системы уравнений:

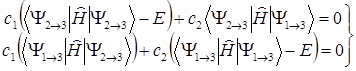(1.11)

Энергии возбужденных состояний можно найти из уравнения:

или

(1.12)

При таком конфигурационном взаимодействии происходит расщепление первоначальных уровней, так что их центр тяжести остается на месте. Это можно показать на такой схеме:

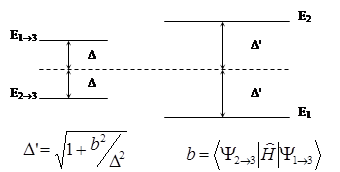(1.13)

Расщепление уровней наблюдается, если b¹0, поэтому смешивающиеся волновые функции должны иметь одну и ту же симметрию.

Дата добавления: 2015-07-11