
Читайте также:
|
Распишем каждое слагаемое в отдельности.
Прибыль от продажи товара за день вычисляется путем суммирования прибыли за каждый час (прибыль в час есть произведение количества всех купленных товаров на среднюю стоимость единицы товара).
Затраты на персонал делятся на две составляющие:
1) почасовая з/п «основных» работников,
2) почасовая з/п работников «на замене», т.е. тех, кто работает во время обеда «основных».
Рабочий процесс установим таким образом, чтобы сотрудники уходили на обед по очереди. Время работы супермаркета пусть будет с 8 до 22 часов. Тогда целесообразно установить обеденное время с 12 до 18 часов. Таким образом, на замене с 12 до18 часов должен быть лишь 1 человек каждого из рассматриваемых профессий на 6 человек персонала. Пусть  - количество кассиров, доставщиков и кладовщиков за день, работающих не «на замене», соответственно. Тогда в случае кассиров:
- количество кассиров, доставщиков и кладовщиков за день, работающих не «на замене», соответственно. Тогда в случае кассиров:  - необходимое число работников «на замене». В случае кладовщиков и доставщиков получаем абсолютно аналогичные результаты.
- необходимое число работников «на замене». В случае кладовщиков и доставщиков получаем абсолютно аналогичные результаты.
Недополученная прибыль определяется количеством товаров, которое не смогли приобрести покупатели, имея такое желание. Т.е. она появляется, когда спрос не удовлетворен. В модели спрос – это случайная величина, а значит, требуется сначала обработать статистику и построить примерный закон ее распределения. Но даже в случае точного закона нам не удастся всегда его удовлетворять в силу различных факторов.
Итак, основываясь на вышесказанном, мы приходим к следующему виду целевой функции:

или

Как видно, целевая функция зависит от случайных величин. Поэтому возьмем математическое ожидание (т.е. ожидаемую прибыль) в качестве максимизируемой функции.


 Величины
Величины  в соответствии с постановкой задачи удовлетворяют условиям
в соответствии с постановкой задачи удовлетворяют условиям 
Будем считать, что величины  - независимые,
- независимые,  - независимые, а также они независимы в совокупности. Тогда
- независимые, а также они независимы в совокупности. Тогда  . Пусть также
. Пусть также 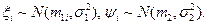 Получаем:
Получаем:
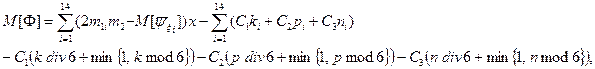
Запишем теперь ограничения.
1)  - время обслуживания всех покупателей всеми работающими кассирами в
- время обслуживания всех покупателей всеми работающими кассирами в  -ый час. Тогда получаем двойное неравенство:
-ый час. Тогда получаем двойное неравенство:

Условие с максимальным временем дает нам ограниченность очереди, а условие с минимальным временем – ограничение снизу на производительность.
2) Условие на наличие товара на полках в торговом зале запишем в виде:


3) Условие на работу кладовщиков:
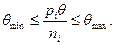
Здесь аналогично условию 1) левое неравенство дает ограничение на производительность труда, а правое – на длину очереди (или время обслуживания).
Преобразуем полученные ограничения.
1) 
 тогда приходим к ограничениям
тогда приходим к ограничениям

2) 
3) 
Потребуем выполнение этих ограничений с вероятностью  , близкой к 1. Численное значение
, близкой к 1. Численное значение  выберем из следующих соображений. Пусть
выберем из следующих соображений. Пусть  - примерные доходы гипермаркета за день,
- примерные доходы гипермаркета за день,  - доходы гипермаркета с экстремальными расходами (вызов дополнительных сотрудников или плата за внеурочную работу). Тогда уравнение баланса будет иметь вид:
- доходы гипермаркета с экстремальными расходами (вызов дополнительных сотрудников или плата за внеурочную работу). Тогда уравнение баланса будет иметь вид:
 откуда получаем выражение для
откуда получаем выражение для  :
:

Приходим к виду:


Последние два неравенства из вероятностных ограничений зависят от количества доставщиков  , ограничение на которое описывается выше. Такая ситуация не типична для вероятностных ограничений, поэтому уберем явную зависимость одной переменной от другой. Для этого воспользуемся доверительным подходом. Построим для
, ограничение на которое описывается выше. Такая ситуация не типична для вероятностных ограничений, поэтому уберем явную зависимость одной переменной от другой. Для этого воспользуемся доверительным подходом. Построим для  и
и  доверительные множества
доверительные множества  .
.

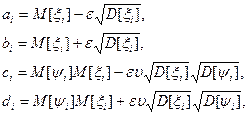
или, учитывая принятые допущения,

Параметры  и
и 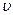 выбирается так, чтобы мера исходного многомерного множества была равной
выбирается так, чтобы мера исходного многомерного множества была равной  . Если воспользоваться правилом «трех сигм», то мера 14-мерного множества будет равной 0,9629. Будем считать
. Если воспользоваться правилом «трех сигм», то мера 14-мерного множества будет равной 0,9629. Будем считать  =0,9629 приемлемым результатом, так как «экстренные» случаи при таком выборе будут происходить крайне редко. Таким образом, полагаем
=0,9629 приемлемым результатом, так как «экстренные» случаи при таком выборе будут происходить крайне редко. Таким образом, полагаем  =3.
=3.
Тогда вероятностные ограничения запишутся в виде:
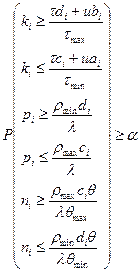
Пример.
Рассмотрим модель со следующими параметрами:
 руб/час,
руб/час,  руб/час,
руб/час,  руб/час;
руб/час;
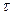 =20 сек=1/3мин, u=45 сек=3/4мин;
=20 сек=1/3мин, u=45 сек=3/4мин;
 =100 ед.,
=100 ед.,  =3 мин.
=3 мин.

 =15 ед.,
=15 ед.,  =
=  =0,01.
=0,01.
Пусть средняя проходимость магазина в час равна 1500 человек, тогда имеем:
| Часы работы | 
| 
|
| 8-9 | ||
| 9-10 | ||
| 10-11 | ||
| 11-12 | ||
| 12-13 | ||
| 13-14 | ||
| 14-15 | ||
| 15-16 | ||
| 16-17 | ||
| 17-18 | ||
| 18-19 | ||
| 19-20 | ||
| 20-21 | ||
| 21-22 |
 55 мин,
55 мин,  20 мин;
20 мин;

 ,
, 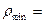
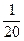 ;
;
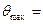 55 мин,
55 мин,  20 мин;
20 мин;
Дата добавления: 2015-07-11; просмотров: 55 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Специфика формата | | | ВВЕДЕНИЕ |