Основы работы с MS Excel

«Атомарным» элементом электронной таблицы MS Excel является ячейка (cell) – поле для ввода данных различных типов (числовой, денежный, дата, время, текстовый, процентный, экспоненциальный и т.д.). Каждая ячейка имеет собственное уникальное имя, получаемое при указании строки и столбца, на пересечении которых она находится. В одну ячейку таблицы может быть записано только одно значение соответствующего типа данных. Благодаря этим принципам функционирования таблиц, мы имеем возможность обратиться к любому элементу данных.

В Excel существует возможность объединения нескольких ячеек в одну (группировка). При необходимости получения данных из сгруппированных ячеек следует обратиться к первой (левой верхней) ячейке группы. Если же обратиться к любой другой ячейке группы, то это не вызовет ошибки, но возвращаемое значение будет равно нулю.

Чтобы в ячейке таблицы получить некоторое значение, вычисляемое на основе данных их других ячеек, необходимо указать функцию в строке формул, находящейся над рабочей областью электронной таблицы. Перед вводом любой формулы необходимо ставить знак равенства “ = ”.

Адресация ячеек может быть относительной и абсолютной. Абсолютная адресация используется для многократных вычислений с содержимым адресуемой ячейки на некотором множестве. Может задаваться, например, так: =2*$C$2, т.е. знак “$” выполняет роль фиксатора для указателя на адрес ячейки. При такой записи все вычисления, связанные с автоматическим заполнением ряда данными будут производиться только с ячейкой C2. Относительная адресация позволяет варьировать адрес при заполнении некоторого ряда данных. Комбинирование абсолютного и относительного адресов в вычисляемой формуле позволяет корректно указать табличному процессору порядок заполнения ряда данных.

строка формул

Рисунок 1

Чтобы заполнить некоторое множество ячеек данными, вычисляемыми по одной и той же формуле, необязательно записывать её в каждую ячейку, а достаточно указать её лишь в одной ячейке, правильно применив, оператор фиксации “$”. Потянув за правый нижний уголок ячейки с формулой можно сформировать желаемый ряд данных с использованием относительной адресации.

Подробную информацию об имеющихся функциях и их синтаксисе всегда можно найти в файлах справки табличного процессора MS Excel или при вызове мастера вставки функции (кнопка f_x перед строкой формул).

MS Excel имеет мощные средства форматирования данных и документов, обширную библиотеку стилей и шаблонов, развитые средства визуализации данных (построение диаграмм, подключение сторонних графических объектов и программных модулей), возможность сетевой поддержки таблиц (распределённый доступ к таблице по сети, получение данных из других таблиц) и др.

Аппроксимация дискретных данных с использованием метода наименьших квадратов (МНК)

Аппроксимация (лат. approximare – «приближаться») – замена одних математических объектов другими, в том или ином смысле близкими к исходным.

Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны). В нашем задании будем рассматривать частный случай аппроксимации – аппроксимацию экспериментальных данных и кривых, построенных на их основе.

Рассмотрим типовую задачу аппроксимации в инженерной практике – подбор математического выражения, описывающего связь между экспериментальными данными. Само математическое выражение называют уравнением регрессии (регрессией), а соответствующую кривую – линией регрессии. Чтобы подобрать наилучшую в некотором смысле регрессию, необходимо установить критерий оптимального её выбора. Одним из широко применяемых на практике критериев оптимальности регрессии является критерий минимума суммы квадратов. В соответствии с этим критерием наилучшее согласование линии регрессии с результатами измерения достигается при выполнении условия:

, (1)

где – уравнение регрессии,

– дискретное множество экспериментальных данных.

Его применение позволяет при определении линии регрессии использовать метод наименьших квадратов, обеспечивающий построение линии регрессии, характеризуемой минимальным средним квадратом её отклонения от результатов эксперимента.

После определения критерия оптимальности регрессии следует перейти к выбору типа уравнения регрессии. Тип уравнения в значительной мере зависит от вида экспериментальных данных.

Далее необходимо найти конкретные значения параметров уравнения регрессии, в общем случае составив систему уравнений вида:

, (2)

где Q – математическая запись выбранного критерия,

p_i – параметры уравнения регрессии.

Функции MS Excel, используемые в работе

· ИНДЕКС - возвращает значение или ссылку на значение из таблицы или диапазона. Функция ИНДЕКС имеет две формы: ссылочную и форму массива.

· ЛИНЕЙН - функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую. Функцию ЛИНЕЙН также можно объединять с другими функциями для вычисления других видов моделей, являющихся линейными по неизвестным параметрам, включая полиномиальные, логарифмические, экспоненциальные и степенные ряды.

· ЛГРФПРИБЛ - в регрессионном анализе вычисляется экспоненциальная кривая, аппроксимирующая данные, и возвращается массив значений, описывающий эту кривую.

· СУММ - функция СУММ вычисляет сумму всех чисел, указанных в качестве аргументов. Каждый аргумент может быть диапазоном, ссылкой на ячейку, массивом, константой, формулой или результатом другой функции.

· НОРМРАСП - возвращает нормальную функцию распределения для указанного среднего и стандартного отклонения.

· СТЕПЕНЬ - возвращает результат возведения числа в степень.

· КОРЕНЬ - возвращает положительное значение квадратного корня.

Расчетные формулы

· Выборочное среднее:

n_i – частота события x_i;

n – объём выборки (общее количество замеров), ;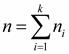

k – количество различных значений измерений.

· Исправленная выборочная дисперсия:

.

· «Исправленное» с. к. о.:

.

· Плотность нормального распределения случайной величины Х:

Дата добавления: 2015-07-11