
|
Читайте также: |
1. Построение алгоритмов ветвящейся и циклической структуры.
(с использованием одномерных массивов)
2. Вложенные циклы. (с использованием двухмерных массивов)
| Даны натуральные числа n, a1, a2, …,an. Определить количество ak последовательности a1,a2,…,an являющихся нечётными числами | |
| Дана действительная матрица размера m´n. Определить числа b1,…,bm равные суммам элементов строк. | |
| Даны натуральные числа n, a1, a2, …,an. Определить количество ak последовательности a1,a2,…,an кратных 3 и не кратных 5. | |
| Дана действительная матрица размера m´n. Определить числа b1,…,bm равные произведениям элементов строк. | |
| Даны натуральные числа n, a1, a2, …,an. Определить количество ak последовательности a1,a2,…,an являющихся квадратами чётных чисел. | |
| Дана действительная матрица размера m´n. Определить числа b1,…,bm равные наименьшим значениям элементов строк. | |
Даны натуральные числа n, a1, a2, …,an. Определить количество ak последовательности a1,a2,…,an удовлетворяющих условию
 . .
| |
| Дана действительная матрица размера m´n. Определить числа b1,…,bm равные значениям средних арифметических элементов строк. | |
Даны натуральные числа n, a1, a2, …,an. Определить количество ak последовательности a1,a2,…,an удовлетворяющих условию
 . .
| |
| Дана действительная матрица размера m´n. Определить числа b1,…,bm равные разностям наибольших и наименьших значений элементов строк. | |
| Даны натуральные числа n, q1, q2,…, qn. найти те члены qi последовательности q1, q2,…, qn которые являются удвоенными нечётными числами. | |
| Даны натуральное число n, действительная матрица размера n´9. найти средне арифметическое: а) каждого из столбцов; б) каждого из столбцов, имеющих чётные номера. | |
| Даны натуральные числа n, q1, q2,…, qn. найти те члены qi последовательности q1, q2,…, qn которые при делении на 7 дают остаток 1.2 или 5. | |
Даны целые числа а1, а2, а3. Получить целочисленную матрицу  , для которой , для которой  . .
| |
Даны натуральные числа n, q1, q2,…, qn. найти те члены qi последовательности q1, q2,…, qn которые обладают тем свойством, что корни уравнения 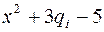 действительны и положительны. действительны и положительны.
| |
Даны действительные числа а, …,а; b, …,b. Получить действительную матрицу 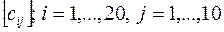 , для которой , для которой 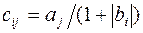 . .
| |
Дано натуральное число n. Получить сумму тех чисел вида  , которые являются удвоенными нечётными. При отсутствии таких чисел искомая сумма равна нулю. , которые являются удвоенными нечётными. При отсутствии таких чисел искомая сумма равна нулю.
| |
Дано натуральное число n. получить действительную матрицу 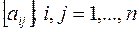 , для которой , для которой
 . .
| |
| Даны целые числа а1,…,а50. Получить сумму тех чисел данной последовательности, которые кратны 5. | |
Получить 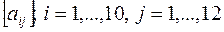 - целочисленную матрицу для которой - целочисленную матрицу для которой  . .
| |
| Даны целые числа а1,…,а50. Получить сумму тех чисел данной последовательности, которые нечётны и отрицательны. | |
Получить действительную матрицу  , первая строка которой задаётся формулой , первая строка которой задаётся формулой  , вторая строка задаётся формулой , вторая строка задаётся формулой  , а каждая следующая строка есть сумма двух предыдущих. , а каждая следующая строка есть сумма двух предыдущих.
| |
Даны целые числа а1,…,а50. Получить сумму тех чисел данной последовательности, которые удовлетворяют условию  . .
| |
Дано натуральное число n. Выяснить сколько положительных элементов содержит матрица 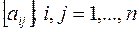 , если , если  . .
| |
| Даны натуральное число n, действительные числа a1, a2, …,an. в последовательности a1, a2, …,an все отрицательные члены увеличить на 0.5, а все неотрицательные заменит на 0.1. | |
| Дана действительная матрица n´m, в которой не все элементы равны нулю. Получить новую матрицу путём деления всех элементов данной матрицы на её наибольший по модулю элемент. | |
| Даны натуральное число n, действительные числа x1,…xn. В последовательности x1,…xn все члены меньшие двух, заменить нулями. Кроме того, получить сумму членов, принадлежащих отрезку [3,7], а также число таких членов. | |
| Дана действительная квадратная матрица порядка 12. Заменить нулями все её элементы, расположенные на главной диагонали и выше неё. | |
| Даны натуральные числа n, a1, a2, …,an. В последовательности a1, a2,…,an все неотрицательные члены, не принадлежащие отрезку [1,2], заменить на единицу. Кроме того получить число отрицательных членов и число членов, принадлежащих отрезку [1,2]. | |
Даны действительные числа х1,…,х8. Получить действительную квадратную матрицу порядка 8:
а)  б) б) 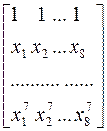 . .
| |
| Даны натуральные числа n, a1, a2, …,an. В последовательности a1, a2,…,an получить сумму положительных и число отрицательных членов. | |
Даны натуральное число n, действительная матрица 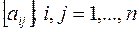 . Получить последовательность элементов главной диагонали а11, а22,…, аnn. . Получить последовательность элементов главной диагонали а11, а22,…, аnn.
| |
| Даны натуральные числа n, a1, a2, …,an. Заменить все большие семи члены последовательности a1, a2, …,an числом 7. Вычислить количество таких членов. | |
| Дана действительная матрица размера 6´9. Найти среднее арифметическое наибольшего и наименьшего значений её элементов. | |
| Даны целые числа a1, a2, …,a45. Получить число отрицательных членов последовательности a1, a2, …,a35 и число нулевых членов всей последовательности a1, a2, …,a45. | |
Дана действительная квадратная матрица 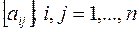 . Получить две квадратные матрицы . Получить две квадратные матрицы  ; ;  , для которых , для которых
 . .
| |
Пусть  Дано неотрицательное целое число n, действительные a, b, c, d, q (c<d). Принадлежит ли Дано неотрицательное целое число n, действительные a, b, c, d, q (c<d). Принадлежит ли 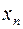 интервалу (c,d)? интервалу (c,d)?
| |
Для заданных а и b определить  . .
| |
| Даны целые числа а1,…,а50. Получить последовательность b1,…,b50, которая отличается от исходной тем, что все члены удвоены. | |
| Дана действительная матрица 18´n. Найти значение наибольшего по модулю элемента матрицы, а также индексы данного элемента. | |
Вычислить  , где , где
 . .
| |
| Дана действительная матрица размера m´n. Найти сумму наибольших значений элементов её строк. | |
Даны натуральные числа n, b0,…,bn. Вычислить f(b0)+f(b1)+…+f(bn), где
 . .
| |
| В данной действительной квадратной матрице порядка n найти сумму элементов строки, в которой расположен элемент с наименьшим значением. Предполагается, что такой элемент единственный. | |
| Даны целые числа a, n, x1,…,xn (n>0). Определить, каким по счёту идёт в последовательности x1,…,xn член, равный а. Если такого члена нет, то ответом должно быть число 0. | |
| В матрице с размерности (4´4) вычислить сумму произведений элементов каждой строки. | |
| Даны натуральное число n, действительные числа a1, a2, …,an. Получить max(a1, a2, …,an). | |
| В массиве данных с1, …,с20 определить сумму квадратов отрицательных элементов и сумму положительных. Подсчитать количество положительных, отрицательных и нулевых элементов. | |
| Даны натуральное число n, действительные числа a1, a2, …,an. Получить min(a1, a2, …,an). | |
Сформировать массив р из 20 элементов, i-ый элемент которого определяется по формуле  , где х=0ю225. Расставить в порядке возрастания элементы массива. , где х=0ю225. Расставить в порядке возрастания элементы массива.
| |
| Даны натуральное число n, действительные числа a1, a2, …,an. Получить max(a2, a4, …). | |
| задана матрица размерности (5´6). Если минимальный элемент в строке матрицы меньше 1, то элементы в этой строке заменить нулями. | |
| Даны натуральное число n, действительные числа a1, a2, …,an. Получить min(a1, a3, …). |
В массиве a1, a2, …,a10 определить максимальную из сумм (аi+aj), где 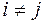 , а также определить номера этих элементов. , а также определить номера этих элементов.
| |
| Даны натуральное число n, действительные числа a1, a2, …,an. Получить min(a2, a4, …)+ max(a1, a3, …) | |
| Для массива a1, a2, …,a10 найти сумму элементов с нечётными индексами. Если она окажется больше 10, то значения этих элементов положить равными 1. | |
| Даны натуральное число n, действительные числа a1, a2, …,an. Получить max(ça1ç, ça2ç, …,çanç). | |
| заданы элементы массива a1, a2, …,a10 и b1, b2, …,b10. Получить массив z, каждый элемент которого определяется как максимальное значение из соответствующих элементов. |
Дата добавления: 2015-07-11; просмотров: 148 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Постановка задачи. | | | ОПРЕДЕЛЕНИЯ |