СД алгоритмі

Бұл алгоритм былай жұмыс істейді. Бірінші кезекте ақпаратты таратуға кететін шығындарды азайта отырып бір-біріне жақын орналасқан әр төбе үшін еңкіші негізгі G ішграфы тұрғызылады. Бұл кезде алгоритмнің барлық орындамалық шығын матрицасына жүргізіледі. Егер ең кіші G ішграфындағы x_i және x_j төбелері бір-бірімен байланысқан болса онда x_ij айнымалысы 1-ге тең, олай болмаса 0-ге тең. Алынған ең кіші G ішграфтың ең жақын негізі болуы үшін 1 тең х айнымалыларының саның анықтаса және N=2(m-1) шартын тексерсе жеткілікті. Егер теңдік қаңағаттандырылса онда алынған ішгарф ең жақын болып табылады. Олай болмаған жағдайда графтың жақын негізінің төбелерінің бір-бірімен байланыстығы тексеріледі, яғни осындай графтын кез келген екі төбесі тек бір мақсатпен ғана табылу керек. Ол үшін граф төбелерінің дәрежелері есептелуі қажет содан кейін дәрежелер саны бірден көп төбелердің бір-бірімен байланыстығы тексеріледі. Егер олардың арасында байланыссыз төбелер болса мұнда оларды байланыстыратын көп жолдардың ішінен жалпы салмағы ең аз тек жалғыз жол анықталады. Бұл кезде бұл жолға сәйкес келетін айнымалы 1 теңестіріледі.

Бұл әрекет байланыссыз төбелердың бәріне істелінеді. Содан кейін N=2(m-1) шартының орындалуын тексереміз. Егер шарт орындалмаса графтың басқа төбелерімен байланыспаған дәрежесі 1 тең шеткі төбелер үшін оқшауланған қабырғалар (ребро) ізделінеді. Бұл кезде бұл төбелер үшін x_ij=x_ji=1, ал қалған айнымалылар x_ik=x_jl=0 (k¹i, j¹l, kÎM_i, lÎM_j) оқшауланған қабырға бар болған кезде оның әр төбесі үшін ең аз салмақты жақын тұрған төбемен байланысы анықталады, яғни 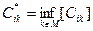және содан кейін ñ,ñ анықталады және х _і-2 төбе төбемен біріктіріледі.

Осындай әрекетті оқшауланған қабырғаның қалған төбелерінде қолданà аламыз. Бұл үдеріс N=2(m-1) шарты орындалғанша жалғаса береді.

Енді алгоритмді қадамы бойынша жазамыз:

1 қадам. N=0 анықтау

2 қадам. Әр бағана үшін j=1 бастапқы және iÎm болған кездегі клеткаларын анықтау керек айнымалларын теңестіруі керек, ал қалғандарын x_ij=0 теңестіру керек.

3 қадам. N=N+2 және j=j+1 жаңа мәндерін анықтау керек. Егер j£m балса онда екінші қадамға өту керек.

4 қадам. Егер N=2(m-1) болса 11 қадамға өту керек.

5 қадам. Әр бағанаға сәйкес келетін графтың төбелерінің дәрежесін айнымалылар мәні бір-біріне қосу арқылы есептеу керек, яғни

6 қадам. Дәреже саны бір жоғары õ_j1 және õ_j2 төбелерінің нөмерлерін өсу реті бойынша таңдау керек.

егер болса, онда дәрежелер 1 жоғары келесі екі төбені таңдап тексеруді қайталау керек. Егер дәрежелері 1 жоғары барлық төбелер қарастырылса онда 8 қадамға өту керек, ал олай болмаса 7 қадамға өту керек.

7 қадам. және көп мүшелерінің төбелерін жалғастыратын салмағы ең аз қабырғаны анықтау керек. N=N+1, x_j*i*=1 анықтау керек. 6 қадамға өту керек.

8 қадам. егер N=2(m-1) болса онда 11 қадамға өту керек.

9 қадам. Шеткі төбелері x_ik=x_jl=0 (k¹i, j¹l, kÎM_i, lÎM_j) және дәрежелері 1 тең оқшауланған қабырғаларды анықтау керек. 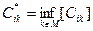және анықтау керек.

10 қадам. Егер 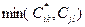, болса онда және деп қабылдау керек. 8 қадамға өту керек.

11 қадам. Алгоритмнің соңы.

Дата добавления: 2015-10-16