Мева года

Мева следуют в обратном порядке (от 9 до 1) и сменяются ежегодно, так что через каждые 9 лет цикл Мева повторяется. Как уже отмечалось во вводной части, комбинация Мева-животное-элемент года (скажем, год Водяного дракона с Мева 3) повторяется каждые 180 лет. При этом каждому животному могут соответство­вать только три значения Мева, а другие никогда не выпадают:

Мева тигра, обезьяны, свиньи и змеи могут быть 2, 5, 8; Мева мыши, лошади, петуха и зайца могут быть 1,4, 7; Мева быка, овцы, собаки и дракона могут быть 3, 6, 9.

Цикл 180 лет Мекор (sme 'khor) включает в себя три 60- лет­них цикла Метрэнг (sme phreng), которые называют верхним, средним и нижним:

верхний цикл начинается годом Деревянной мыши с Мева 1;

средний цикл начинается годом Деревянной мыши с Мева 4;

нижний цикл начинается годом Деревянной мыши³³ с Мева 7.

В табл. 5п в приложении приведены значения Мева для годов текущего 180-летнего цикла, который начался в 1864 году и завершится в 2043-м. Поскольку каждые 180 лет комбинация Мева- животное-элемент повторяется, с помощью этой таблицы можно определить Мева для любого года прошлого или будущего. Нужно лишь определить с помощью таблицы 2п комбинацию животное-элемент года, затем определить, отсчитав циклы, к какому цикл (верхнему, среднему или нижнему) относится данный год, поош чего воспользоваться табл. 5п.

[33] Обратите внимание на то, что верхний, средний и нижний циклы начинаются го- дом Деревянной мыши, а не Огненного зайца, как в официальном тибетском летоисчислении. Это связано с тем, что система исчисления 180-летних циклов су­ществовала в Тибете еще до прихода в Тибет учений Калачакры (1027г.), и начало циклов в ней соответствует началу 60-летних циклов в китайской традиции. Тибет­ское же официальное летоисчисление основано на системе Калачакры, что и обуславливает сдвиг на 3 года (см. выше). В любом случае этот сдвиг не может вызвать путаницы, так как он связан лишь с формальным определением начала цик-ла и не влияет на порядок следования комбинаций животное-элемент, характеризующих каждый год.

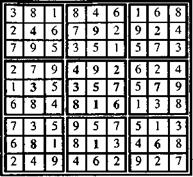
Рис. 6. Диаграмма девяти магических квадратов

Дата добавления: 2015-10-16