Теоретическое введение. Определение модуля сдвига материала и момента инерции тела сложной формы методом

ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА МАТЕРИАЛА И МОМЕНТА ИНЕРЦИИ ТЕЛА СЛОЖНОЙ ФОРМЫ МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ

Цель работы: изучение крутильных колебаний тонкого стержня (проволоки), определение модуля кручения и модуля сдвига испытуемой проволоки, идентификация материала по его модулю сдвига, овладение одним из методов определения момента инерции.

Оборудование: лабораторный стенд, закрепленный на нем горизонтальный стержень с отверстием для крепления проволоки, секундомер, проволока с закрепленным на ней цилиндром – крутильный маятник, тело сложной формы, линейка, штангенциркуль, микрометр.

Теоретическое введение

Деформации растяжения, сжатия, сдвига представляют собой деформации однородные, т. е. такие, когда все бесконечно малые элементы тела деформируются одинаково. Деформации кручения и изгиба являются деформациями неоднородными. Это значит, что в этих случаях деформации внутри тела меняются от точки к точке.

Возьмем однородную проволоку, закрепим ее верхний конец, а к нижнему концу приложим закручивающие силы, создающие вращающий момент М относительно продольной оси проволоки. Проволока закрутится – каждый радиус нижнего основания ее повернется вокруг продольной оси на угол φ. Такая деформация называется кручением. Опыт показывает, что момент упругих сил М,стремящийся вернуть тело в положение равновесия, в довольно широких пределах пропорционален углу φ. Закон Гука для деформации кручения записывается в виде:

М = – f φ, (4.1)

где f – постоянная для данной проволоки величина, называемая ее модулем кручения. Модуль кручения зависит не только от материала, но и от геометрических размеров проволоки.

Выведем выражение для модуля кручения f. Сначала сделаем это для цилиндрической трубки радиусом r и длиной l, предполагая, что толщина δ r стенки трубки очень мала по сравнению с радиусом r. Площадь основания S трубки есть 2π r δ r. Момент сил, действующий на это основание, будет М = 2π r δ r ∙ τ r, где τ – касательное напряжение в том же основании. При квазистатическом закручивании проволоки на угол φ совершается работа A = (l/2) M φ = M ²/2 f. Разделив ее на объем трубки V = 2π rl δ r,найдем плотность упругой энергии при деформации кручения

. (4.2)

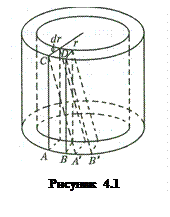Ту же величину можно выразить иначе. Вырежем мысленно из трубки бесконечно короткую часть, изображенную на рис. 4.1. В результате деформации кручения бесконечно малый элемент трубки ABDC перейдет в положение А'В'DC. Это есть сдвиг. Угол АСА' = γ – угол сдвига. Закон Гука в этом случае:

τ = G γ, (4.3)

где постоянная G называется модулем сдвига и зависит только от материала, из которого изготовлена трубка. При квазистатическом сдвиге вся работа, затрачиваемая на сдвиг, очевидно, пойдет на увеличение упругой энергии тела: A = (l/2)τ S АА'. Здесь АА' ≈ АС γ. Тогда A = (l/2)τ S АС γ = (l/2)τ V γ. Отсюда с учетом (4.3) объемная плотность упругой энергии

. (4.4)

Таким образом, деформацию кручения можно рассматривать как неоднородный сдвиг. Приравнивая выражения (4.2) и (4.4), находим искомое соотношение

. (4.5)

Если стенка трубки имеет конечную толщину, то модуль f найдется интегрированием последнего выражения по r. Это даёт

, (4.6)

где r ₁ – внутренний радиус трубки, а r ₂ – наружный. Для сплошной проволоки радиуса r

. (4.7)

Здесь d – диаметр проволоки.

Экспериментально модуль кручения можно измерить, наблюдая крутильные колебания тяжелого тела, подвешенного к нижнему концу проволоки. Из динамического уравнения (4.1) следует, что , откуда вытекает дифференциальное уравнение движения крутильного маятника:

. (4.8)

Очевидно, что эти колебания будут гармоническими с периодом

. (4.9)

Дата добавления: 2015-10-16