Теоретическое введение

Определение модуля сдвига материала методом крутильных колебаний

Цель работы: изучение крутильных колебаний тонкого стержня, определение модуля кручения и модуля сдвига испытуемого стержня, идентификация материала по его модулю сдвига.

Оборудование: платформа на регулирующихся ножках, закрепленная на ней стойка со шкивом и угломерной шкалой на конце; закрепленные на платформе часы-таймер; кронштейн для крепления испытуемого стержня к стойке установки; кронштейн для крепления на испытуемом стержне тяжелой балки с отверстиями, два тонких круглых стержня в качестве образцов для испытаний; два массивных груза с штырями для крепления их на балке.

Теоретическое введение

Деформации растяжения, сжатия, сдвига представляют собой деформации однородные, т. е. такие, когда все бесконечно малые элементы тела деформируются одинаково. Деформации кручения и изгиба являются деформациями неоднородными. Это значит, что в этих случаях деформации внутри тела меняются от точки к точке.

Возьмем однородную проволоку, закрепим ее верхний конец, а к нижнему концу приложим закручивающие силы, создающие вращающий момент М относительно продольной оси проволоки. Проволока закрутится – каждый радиус нижнего основания ее повернется вокруг продольной оси на угол φ. Такая деформация называется кручением. Опыт показывает, что момент упругих сил М,стремящийся вернуть тело в положение равновесия, в довольно широких пределах пропорционален углу φ. Закон Гука для деформации кручения записывается в виде:

М = – f φ, (1)

где f – постоянная для данной проволоки величина, называемая ее модулем кручения. Модуль кручения зависит не только от материала, но и от геометрических размеров проволоки.

Выведем выражение для модуля кручения f. Сначала сделаем это для цилиндрической трубки радиусом r и длиной l, предполагая, что толщина δ r стенки трубки очень мала по сравнению с радиусом r. Площадь основания S трубки есть 2π r δ r. Момент сил, действующий на это основание, будет М = 2π r δ r ∙ τ r, где τ – касательное напряжение в том же основании. При квазистатическом закручивании проволоки на угол φ совершается работа A = (l/2) M φ = M ²/2 f. Разделив ее на объем трубки V = 2π rl δ r,найдем плотность упругой энергии при деформации кручения

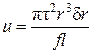. (2)

Ту же величину можно выразить иначе. Вырежем мысленно из трубки бесконечно короткую часть, изображенную на рис. 1. В результате деформации кручения бесконечно малый элемент трубки ABDC перейдет в положение А'В'DC. Это есть сдвиг. Угол АСА' = γ – угол сдвига. Закон Гука в этом случае:

τ = G γ, (3)

где постоянная G называется модулем сдвига и зависит от материала, из которого изготовлена трубка. При квазистатическом сдвиге вся работа, затрачиваемая на сдвиг, очевидно, пойдет на увеличение упругой энергии тела: A = (l/2)τ S АА'. Здесь АА' ≈ АС γ. Тогда A = (l/2)τ S АС γ = (l/2)τ V γ. Отсюда с учетом (3) объемная плотность упругой энергии

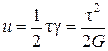. (4)

Таким образом, деформацию кручения можно рассматривать как неоднородный сдвиг. Приравнивая выражения (2) и (4), находим искомое соотношение

. (5)

Если стенка трубки имеет конечную толщину, то модуль f найдется интегрированием последнего выражения по r. Это даёт

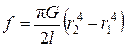, (6)

где r ₁ – внутренний радиус трубки, а r ₂ – наружный. Для сплошной проволоки радиуса r

. (7)

Здесь d – диаметр проволоки.

Экспериментально модуль кручения можно измерить, наблюдая крутильные колебания тяжелого тела, подвешенного к нижнему концу проволоки. Из динамического уравнения (1) следует, что , откуда вытекает дифференциальное уравнение движения крутильного маятника:

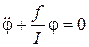. (8)

Очевидно, что эти колебания будут гармоническими с периодом

. (9)

Дата добавления: 2015-10-16