Индекс структурных сдвигов

Выше изложенные общие индексы применимы к изучению явлений, образованных как разными, так и однородными процессами. В послед­нем случае динамику итога можно показать через простые общие ин­дексы отдельных факторов.

Для доказательства в формуле количественного индекса Ласпейреса числитель умножим и разделим на , а знаменатель – на 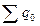. Тогда будем иметь

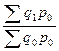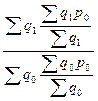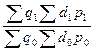= = = , (123)

где 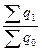= - простой общий индекс количества товаров;

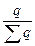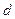= – доля или удельный вес конкретного товара в общем количестве;

= - агрегатный общий индекс структуры, доли или удельного веса, часто называемый индексом структурных сдвигов.

Следовательно, количественный индекс Ласпейреса равняется про­изведению простого общего индекса количества товаров и индекса структурных сдвигов. То есть

= , (124)

откуда для определения индекса структурных сдвигов получается до­вольно простая формула

= / . (125)

Используя формулу (124) в двухфакторной модели общего индекса выручки, получим его трехфакторную мультипликативную модель вида

I_Q = = . (126)

Трехфакторная модель возможна к широкому применению в эконо­мическом анализе для установления количественного влияния каждого фактора на вариацию сложного явления.

---

Дата добавления: 2015-10-16