
Читайте также:
|
Учитывая, что на основе выборочного обследования нельзя точно оценить обобщающую характеристику ГС, необходимо найти пределы, в которых он находится. В конкретной выборке разность 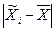 может быть больше, меньше или равна
может быть больше, меньше или равна  . Каждое из отклонений
. Каждое из отклонений 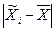 от
от  имеет определенную вероятность. При выборочном обследовании реальное значение
имеет определенную вероятность. При выборочном обследовании реальное значение 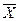 в ГС неизвестно. Зная среднюю ошибку выборки, с определенной вероятностью можно оценить отклонение выборочной средней от генеральной и установить пределы, в которых находится изучаемый параметр (в данном случае среднее значение) в генеральной совокупности. Отклонение выборочной характеристики от генеральной называется предельной ошибкой выборки
в ГС неизвестно. Зная среднюю ошибку выборки, с определенной вероятностью можно оценить отклонение выборочной средней от генеральной и установить пределы, в которых находится изучаемый параметр (в данном случае среднее значение) в генеральной совокупности. Отклонение выборочной характеристики от генеральной называется предельной ошибкой выборки  . Она определяется в долях средней ошибки с заданной вероятностью, т.е.
. Она определяется в долях средней ошибки с заданной вероятностью, т.е.
 = t
= t  , (41)
, (41)
где t – коэффициент доверия, зависящий от вероятности, с которой определяется предельная ошибка выборки.
Вероятность появления определенной ошибки выборки находят с помощью теорем теории вероятностей. Согласно теореме Чебышёва, при достаточно большом объеме выборки и ограниченной дисперсии генеральной ГС вероятность того, что разность между выборочной средней и генеральной средней будет сколь угодно мала, близка к единице:
 при
при  . (42)
. (42)
А. М. Ляпунов доказал, что независимо от характера распределения генеральной ГС при увеличении объема выборки распределение вероятностей появления того или иного значения выборочной средней приближается к нормальному распределению (центральная предельная теорема). Следовательно, вероятность отклонения выборочной средней от генеральной средней, т.е. вероятность появления заданной предельной ошибки, также подчиняется указанному закону и может быть найдена как функция от t с помощью интеграла вероятностей Лапласа:
 , (43)
, (43)
где  – нормированное отклонение выборочной средней от генеральной средней.
– нормированное отклонение выборочной средней от генеральной средней.
Значения P (интеграла Лапласа) для разных t рассчитаны и имеются в специальной таблице, которая приведена в Приложении 1.
Вероятность, которая принимается при расчете выборочной характеристики, называется доверительной. Чаще всего принимают вероятность P = 0,950, которая означает, что только в 5 случаях из 100 ошибка может выйти за установленные границы. Задавшись конкретным уровнем вероятности, выбирают величину нормированного отклонения t по Приложению 1 и рассчитывают предельную ошибку выборки по формуле (41).
После расчета предельной ошибки находят доверительный интервал обобщающей характеристики ГС совокупности по формуле (44) – для среднего значения, и по формуле (45) – для доли единиц, обладающих каким-либо значением признака:
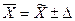 или (
или ( –
–  )
) 
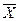
 (
( +
+  )(44)
)(44)
 или (
или ( –
–  )
)  d
d  (
( +
+  ) (45)
) (45)
Следовательно, при выборочном наблюдении определяется не одно, точное значение обобщающей характеристики ГС, а лишь ее доверительный интервал с заданным уровнем вероятности. И это серьезный недостаток выборочного метода статистики.
Дата добавления: 2015-10-16; просмотров: 104 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Средняя ошибка выборки | | | Необходимая численность выборки |