Расчет мощности передатчиков спутниковых линий навигации

Следует определить значения мощности бортового передатчика, при котором он не содержит излишних энергетических запасов, а пользовательский приемник надежно работает в условиях помех.

Рассмотрим структурную схему линии передачи навигационного сигнала и диаграмму уровней сигналов на этом участке, приведенную на рисунке 8.3.

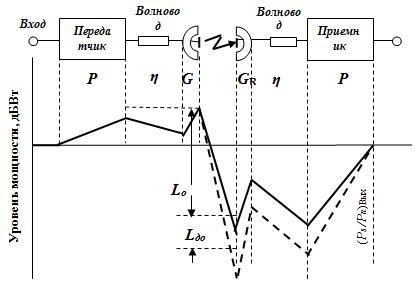
(Р_s/P_n)_вх и (Р_s/P_n)_вых - отношения сигнал/шум на входе и выходе приемника.

Рисунок 8.3 – Эпюры мощностей в канале НКА - потребительский приемник.

Выведем расчетные формулы:

Эквивалентная изотропно излучаемая мощность (ЭИИМ):

Р _eff = Р_T × η _T × G _T,

где Р_T – эффективная мощность на выходе передатчика;

η_T – коэффициент передачи (по мощности) волноводного тракта;

G_T – коэффициент усиления передающей антенны относительно изотропного излучателя.

Ослабление мощности сигнала за счет сферической расходимости фронта волны:

L _o =16π² d ²/ λ ²,

где d – удаление приемникаот НКА и λ – длина волны имеют одинаковую размерность.

Полное ослабление сигнала на пути распространения:

L _Р(дБ) = L _o + L_доп,

где L_доп –дополнительные потери на трассе (поглощение энергии сигнала в атмосфере, потери из-за рефракции, потери из-за несогласованности поляризации антенн и др.) заметного влияния на энергетику спутниковых линий не оказывают.

Мощность сигнала на входе приемника:

. (8.11)

При расчете линии часто задается не мощность сигнала на входе приемника, а отношение сигнал/шум, поэтому в формулу (8.11) следует подставить

Р _R = Р _s (Р_s/Р_n)_imp,

где Р _n= k T _S ∆ f _n – полная мощность шума на входе приемника;

k =1,38×10^-23 Вт/Гц×град - постоянная Больцмана;

T _S - эквивалентная шумовая температура приемного тракта;

∆ f _n – шумовая полоса приемника; Гц

Т _S= Т _А+ Т ₀[(1- η)/ η ]+ T _R/ η.

Т _А- шумовая температура антенны (T _S включает космическое радиоизлучение, излучение атмосферы, земной поверхности, собственные шумы антенны);

T _o≈290K;

Т _R- собственная шумовая температура приемника.

Подставив Р _R и разрешим уравнение (8.11) относительно искомой мощности передатчика R_T:

. (8.12)

8.7 Учет ионосферных поправок

Решая уравнения (8.4-8.6) находим, что поправка к псевдодальности, учитывающая влияние ионосферы, достаточно точно выражается эмпирической формулой

, (8.12)

где k - коэффициент, зависящий от концентрации электронов вдоль трассы распространения сигнала.

Знак в этой формуле зависит от того, какой сигнал используется для вычисления псевдодальности: фаза несущей частоты или кодовая последовательность, содержащая группу волн в некоторой полосе частот. Пер­вому случаю соответствует фазовая скорость распространения, второму - групповая скорость, меньшая по величине. Интересно при этом, что поправки D d_ion оказываются, согласно теории, одинаковыми по абсолют­ной величине в обоих случаях, но при фазовых измерениях их следует вычесть, а при кодовых - прибавить к значению расстояния, рассчитан­ного с использованием значения скорости света в вакууме.

Концентрация электронов на пути следования радиоволн в ионосфе­ре сильно зависит от солнечной активности, от времени года и времени суток, от географического положения станции. Значение поправки D d_ion в направлении зенита может колебаться от 1 до 20 м, а при низких углах наклона радиолуча - достигать 100 м. Это, конечно, очень большие вели­чины, которые надо обязательно каким-то образом учитывать, чтобы не свести на нет высокую точность спутниковых радионавигационных измерений. Существуют для этого два метода: двухчастотный и модельный.

При использовании двухчастотных приемников, способных измерять псевдодальности по кодовым сигналам или по фазе несущей на двух час­тотах f ₁, f ₂, можно так скомбинировать измерения, что влияние ионосферы исключится. Обратимся к выражению для псевдо­дальности, добавив в его правую часть необходимые поправки за влияние ионосферы Dd_ion по формуле (8.12) и тропосферы Dd_tr (о которой поговорим чуть позже). Пусть d¢ ₁и d¢ ₂-результаты кодовых измерений псевдодальности d¢ на двух частотах:

d¢ ₁ =c-c (Dt_R-Dt_S)+ k/f ₁² +Dc_tr,

d¢ ₂ =c-c (Dt_R-Dt_S)+ k/f ₂² +Dc_tr. (8.13)

Если умножить первое из этих выражений на f ₁²/(f ₁²- f ₂²), а второе на -f ₂² / (f ₁²- f ₂²) и затем сложить, то получим:

d¢ ₃ = d- c-c (Dt_R-Dt_S)+ D d_tr. (8.14)

Как видим, комбинированный результат измерения псевдодальности Р ₃действительно не зависит от влияния ионосферы. Точно так же можно образовать комбинированный «ионосферно-независимый» результат фа­зовых измерений L ₃. Собственно говоря, именно ради этого и ведется передача сигналов на двух частотах.

Однако такой метод применим только при работе с фазовыми двухчастотными приемниками, большинство же широко распространенных типов менее дорогих приемников работают только на одной несущей частоте. В таких приемниках учет влияния ионосферы производится с помощью математической моде­ли, текущие параметры которой содержатся в навигационном сообщении. Они вычисляются службой управления на основе собираемой метео­рологической информации. Для вычисления ионосферной задержки Dt_jon используется формула, основанная на модели Дж. А. Клобушара:

Dt_ion= A ₁ + A ₂ × cos[2 p (t-A₃)/A₄],

где А ₁ - задержка кодовых сигналов в ночное время, принимаемая посто­янной и равной 5 нс, а для дневной части суток (от 8 до 20 часов местно­го времени) добавляется второй член, в котором:

А ₃ - постоянная, равная 14 часам;

А ₂ =a ₁+ a ₂ φ_m + a ₃ φ_m ²+ a ₄ φ_m ³;

А ₃ =b ₁+ b ₂ φ_m + b ₃ φ_m ²+ b ₄ φ_m ³;

t - местное время ионосферной точки на линии «спутник-приемник»;

φ_m - геомагнитная широта этой точки.

Коэффициенты a_i, b_i как раз и являются теми величинами, значения которых ежесуточно определяет ведущая станция управления и зак­ладывает на спутники для передачи в составе навигационного сообще­ния. С использованием этих данных и приведенных формул потребитель имеет возможность рассчитать ионосферную поправку Dd_ion = с Dt_ion.

8.8 Определение значения полного электронного содержания в ионосфере

Известно, что при распространении радиосигнала через ионосферу возникает дополнительное групповое (фазовое) запаздывание (ионосферная задержка), величина которого пропорциональна полному электронному содержанию (ПЭС) вдоль траектории распространения радиоволны:

,

Полное электронное содержание – это сумма свободных электронов в столбе, имеющим площадь в 1 м².

Так, при частоте f = 1,6 ГГц (верхняя рабочая частота СРНС), величине ПЭС, равной 1 TECU, соответствует ионосферная задержка Dt_ion = 0,542 нс и приращение группового (фазового) пути Dd_ion = 0,162 м.

На рисунке 8.4 показан образец реконструкции вертикального ПЭС ионосферы Земли на 29 июня 2002 года на 8 ч 4 мин 47 сек (время московское). Черные области соответствуют предельным значениям задержки сигнала в 10 метров по зенитному углу, а белые области – минимальной задержке сигнала.

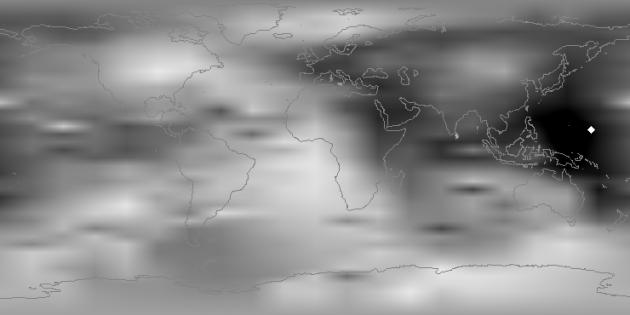
Рисунок 8.4 - Реконструкция полного электронного содержания ионосферы

Анализ приведенных данных ионосферы показывает, что наибольшие значения полной электронной концентрации соответствуют наибольшей освещенности Земли Солнцем (жирная белая точка). Рисунок также демонстрирует, что ионосфера является сложным образованием, пространственное распределение ионизации подчиняется не только суточному ходу. Поэтому постоянный мониторинг состояния ионосферы для получения высоких точностей навигации просто необходим.

8.9 Учет тропосферных поправок

Существуют различные модели тропосферных задержек, отличающи­еся гипотезами о характере изменения метеопараметров с высотой, наи­более употребительными из которых при навигационных измерениях являются две: Хопфилда и Саастамойнена. Приведем формулу для второй из них, что­бы дать представление о подобных моделях, выводимых из уравнений для показателя преломления:

. (8.15)

Здесь z - зенитное расстояние наблюдаемого спутника,

p - атмосфер­ное давление,

Т- температура,

p (H ₂ O) - давление водяных паров (температура выражена в Кельвинах, другие две величины - в миллибарах).

Отметим одно важное обстоятельство: величина тропосферной задерж­ки зависит от угла наклона направления на спутник. Действительно: ведь чем сильнее наклон, тем длиннее путь через тропосферный слой, а верти­кальный луч «прошивает» тропосферу по самому короткому пути. Это нашло отражение и в приведенной выше формуле: когда спутник находит­ся в зените (z = 0), поправка самая маленькая. Указанное обстоятельство позволяет реализовать другой метод определения тропосферных поправок, без измерения метеопараметров. Для этого достаточно найти лишь поправку в зените Dd_tr (0), полагая для других зенитных расстояний

.

Если измерения на пункте продолжаются достаточно долго и наблю­даются спутники при разных углах наклона, то поправку Dd_tr (0) можно определить, включив ее в число неизвестных при совместной обработке измерений методом наименьших квадратов. Такой способ даже точнее, чем по измерениям метеоданных, но его можно применять не в реальном времени в ходе измерений, а только в процессе их постобработки.

При установле­нии этих зависимостей принято рассматривать тропосферу как смесь су­хого воздуха и водяных паров и рассчитывать задержки для каждого из этих компонентов по своим формулам. Отметим, что «сухая» часть за­держки составляет около 90% от полной, и она достаточно точно опреде­ляется по метеоданным, измеренным вблизи приемника. «Влажная» часть зависит от давления водяных паров, которое очень неустойчиво во вре­мени и пространстве.

В среднем тропосферная поправка в зените составляет 2,3 м, а при угле наклона над горизонтом 15° - около 10 м.

Дата добавления: 2015-10-13