
Читайте также:
|
| А | 3,0 | 7,0 | 8,0 | 10,0 | 8,0 |
| 3,0 | Г | 4,0 | 5,0 | 7,0 | 5,0 |
| 7,0 | 4,0 | Е | 1,0 | 3,0 | 1,0 |
| 8,0 | 5,0 | 1,0 | Л | 2,0 | 1,0 |
| 10,0 | 7,0 | 3,0 | 2.0 | М | 2.0 |
| 8,0 | 5,0 | 1,0 | 1,0 | 2,0 | Н |
| Е36 |
Сгруппировав пункты по маршрутам, переходим ко второму этапу.
Этап 2. Определяем рациональный порядок объезда пунктов каждого маршрута. Для этого строим таблицу-матрицу, в которой по диагонали размещаем пункты, включаемые в маршрут, и начальный пункт А, в соответствующих клетках (на пересечении пунктов) — кратчайшие расстояния между ними (табл. 6.6).
Кратчайшее расстояние между А и Г — 3,0 км. Пишем 3,0 на пересечении строк А и Г, под А. Кратчайшее расстояние между А и Е: А-Г + Г-Е = 7,0. Пишем 7,0 на пересечении строк А и Е, под А. Для маршрута А-Л может быть пять вариантов движения:

8,0 км — наименьшее расстояние между А и Л, его и пишем на пересечении строк А и Л, под А. Таким образом заполняется вся матрица.
Начальный маршрут строим для трех пунктов матрицы, из которых один является пунктом отправления, а два

Используя этот метод и формулу приращения, определяем, между какими пунктами расположить пункты Е и Л. Начнем с пункта Л, так как размер суммы этого пункта больше.
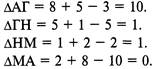
Таким образом, пункт Л включается между пунктами М и А, и из маршрута А-Г-Н-М-А мы получаем маршрут А-Г-Н-М-Л-А.
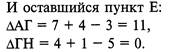
Минимальным значением является ∆ГН == 0, значит, пункт Е включается между пунктами Г и Н. В результате мы имеем оптимальный маршрут развоза продукции А-Г-Е-Н-М-Л-А =3+4+1+2+2+10 =22 км.

Таким же методом определим кратчайший путь объезда пунктов по маршруту 2. В результате расчетов получим маршрут А-В-К-Д-Б-А =1+4+2+2+3= 12 км. Порядок движения по полученным оптимальным маршрутам показан на рис. 6.5.
Дата добавления: 2015-10-13; просмотров: 282 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Методика составления рациональных маршрутов при расчетах вручную | | | Транспортные тарифы и правила их применения |