Доказательство.

База индукции: цикл существует.

Предположим что граф имеющий менее вершин содержит эйлеров цикл.

Рассмотрим связный граф с вершинами, степени которых четны.

Пусть и — вершины графа. Поскольку граф связный, то существует путь из в . Степень — чётная, значит существует неиспользованное ребро, по которому можно продолжить путь из . Так как граф конечный, то путь, в конце концов, должен вернуться в , следовательно мы получим замкнутый путь (цикл). Назовем этот цикл . Будем продолжать строить через таким же образом, до тех пор, пока мы в очередной раз не сможем выйти из вершины , то есть будет покрывать все ребра, инцидентные . Если является эйлеровым циклом для 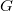, тогда доказательство закончено. 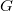Если нет, то пусть — подграф графа , полученный удалением всех рёбер, принадлежащих . Поскольку содержит чётное число рёбер, инцидентных каждой вершине, то каждая вершина подграфа имеет чётную степень. А так как покрывает все ребра, инцидентные , то граф будет состоять из нескольких компонент связности.

Рассмотрим какую-либо компоненту связности . Поскольку рассматриваемая компонента связности имеет менее, чем вершин, а у каждой вершины графа чётная степень, то у каждой компоненты связности существует эйлеров цикл. Пусть для рассматриваемой компоненты связности это цикл . У и имеется общая вершина , так как 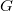cвязен. Теперь можно обойти эйлеров цикл, начиная его в вершине , обойти , вернуться в , затем пройти и вернуться в . Если новый эйлеров цикл не является эйлеровым для 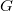, продолжаем использовать этот процесс, расширяя наш эйлеров цикл, пока, в конце концов, не получим эйлеров цикл для .

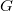Листок 3 (задачи). Подсчёт степеней вершин и обходы. Индукция.

Обходы и подсчёты.

1. В 1905 году был построен Императорский мост, который позже был разрушен бомбардировкой во время Второй мировой войны. Существует легенда о том, что этот мост был построен по приказу самого кайзера, который стал жертвой шутки учёных, бывших на светском приёме. Но, император не растерялся и сказал, что решит эту задачу за одну минуту: для этого ему нужны всего лишь перо и карта города. Ученые даже опешили от такого ответа, но принесли все. Император взял перо и нарисовал еще один мост между островом Ломзе и Форштадтом, сказав: «Повелеваю построить здесь восьмой мост города». На его опорах в 2005 году был построен Юбилейный мост. Изобразите граф мостов и придумайте какой-нибудь способ обхода, добавив 8-й мост там же, где его повелел построить император (Форштадт на схеме внизу реки):

→

2. В шахматном турнире по круговой системе (каждый играет с каждым) участвовало 10 человек. Сколько партий они сыграли друг с другом и сколько сыграл каждый?

3. Может ли в стране, в которой из каждого города выходит ровно три дороги, быть ровно 100 дорог?

4. Докажите лемму о рукопожатиях: в любом графе число вершин нечётной степени всегда чётно, а сумма степеней всех вершин равна удвоенному числу рёбер.

5. В графе каждая вершина покрашена в синий или зеленый цвет. При этом каждая синяя вершина связана с пятью синими и десятью зелеными, а каждая зеленая с девятью синими и шестью зелеными. Каких вершин больше – синих или зеленых?

6. 100 замов получили взыскания от 100 завов. При этом каждый зав наложил по одному взысканию на 15 замов, а каждый зам получил по одному взысканию от 15 завов. Докажите, что директор может снять часть взысканий так, что у каждого зама останется по одному взысканию, и все взыскания будут наложены разными завами.

7. Среди n рыцарей каждые двое – либо друзья, либо враги. У каждого из них ровно 3 врага, причём враги его друзей являются его врагами. При каких n такое возможно?

8. В классе каждый мальчик дружит с тремя девочками, а каждая девочка – с четырьмя мальчиками. 17 из них любят играть в матбой, и в классе 13 столов (за столом сидит 1 или 2 человека). Сколько всего ребят в классе?

9. Артём по одному выставляет королей на шахматную доску, записывая для каждого, сколько ранее выставленных королей он побил. Доска заполнилась. Докажите, что сумма выписанных чисел не зависит от порядка выставления. Чему она равна?

10. В строку выписано 11 целых чисел. Для любой группы подряд идущих чисел подсчитана ее сумма (группы из одного числа тоже учитывались). Какое наибольшее количество сумм могло оказаться нечетными?

Индукция.

1. То, что все лошади одной масти, можно доказать индукцией по числу лошадей в определенном табуне. Вот так: „Если существует только одна лошадь, то она своей масти, так что база индукции тривиальна. Для индуктивного перехода предположим, что существует n лошадей (с номерами от 1 до n). По индуктивному предположению лошади с номерами от 1 до n — 1 одинаковой масти, и, аналогично, лошади с номерами от 2 до n имеют одинаковую масть. Но лошади посредине с номерами от 2 до n — 1 не могут изменять масть в зависимости от того, как они сгруппированы,—это лошади, а не хамелеоны. Поэтому в силу транзитивности лошади с номерами от 1 до n также должны быть одинаковой масти. Таким образом, все n лошадей одинаковой масти – что и требовалось доказать. Есть ли ошибка в приведенном рассуждении и какая именно?

2. Найдите кратчайшую последовательность перекладываний, перемещающих башню из n дисков с левого колышка А на правый колышек В, если прямой обмен дисками между А и В запрещен. (Каждое перекладывание должно производиться через средний колышек. Как обычно, больший диск нельзя класть на меньший.)

3. Покажите, что в процессе перемещения башни при ограничениях из предыдущего упражнения встретятся все допустимые варианты размещения n дисков на трех колышках.

4. Так называемая „диаграмма Венна" с тремя пересекающимися окружностями часто приводится для иллюстрации восьми возможных подмножеств, связанных с тремя заданными множествами:

Можно ли проиллюстрировать четырьмя пересекающимися окружностями шестнадцать возможностей, которые возникают в связи с четырьмя заданными множествами?

5. Некоторые из областей, очерчиваемых п прямыми на плоскости, бесконечны, в то время как другие конечны. Каково максимально возможное число конечных областей?

6. Докажите по индукции равенство: .

7. На плоскости нарисованы несколько окружностей так, что с любой можно перейти на любую, не сходя с этих окружностей. Докажите по индукции, что тогда существует замкнутый путь, проходящий по всем участкам всех окружностей ровно по разу.

8. Докажите по индукции, что если в связном графе степени ровно двух вершин нечетны, то в нем есть эйлеров путь с концами в нечетных вершинах.

9. В стране 100 городов, некоторые из них соединены авиалиниями. Известно, что от любого города можно долететь до любого другого (с пересадками). Докажите с помощью индукции, что можно побывать в каждом не более чем за 196 перелётов.

10. В Вишкилэнде все авиарейсы беспосадочные, летают туда и обратно, и из любого города (с пересадками) можно долететь в любой другой. Все рейсы поделены между двумя компаниями так, что для любой пары городов все прямые рейсы между ними принадлежат только одной компании, и из любого города рейсами одной компании можно улететь в такое же число городов, в какое и рейсами другой компании. Агенту 007 предписано путешествовать, меняя компанию при каждой пересадке. Докажите, что он может из столицы перелететь в любой город.

Дата добавления: 2015-10-13