Листок 2. Графы как иерархии, блок-схемы действий. Деревья. Mind Map.

Древовидная структура является одним из способов представления иерархической структуры в графическом виде. Древовидной структурой он называется благодаря тому, что граф выглядит как перевернутое дерево. По этой же причине говорят, что корневой узел (корень) находится на самом верху, а листья — внизу. Существует множество способов представления древовидных структур.

В подавляющем большинстве случаев они сводятся к различным вариациям или комбинациям нескольких основных стилей:

· Классическая диаграмма со связями между узлами, связывающие попарно узлы при помощи линейных отрезков:

энциклопедия

/ \

наука культура

/ \

искусство ремесло

· Вложенные множества, использующие вложенность друг в друга:

+-------энциклопедия--------+

| +------культура---+ |

| наука |искусство ремесло| |

· Многоуровневая диаграмма-«сосулька», использующая расположения и соседства:

+---------------------------+

| энциклопедия |

+---------+-----------------+

| наука | культура |

+---------+---------+-------+

|искусство|ремесло|

· Диаграммы, использующие отступы, иногда называемые «схемами» или «представлениями деревьев»:

энциклопедия

наука

культура

искусство

ремесло

· Вложенные скобки, впервые предложенные сэром Артуром Кэли:

(наука,(искусство,ремесло)культура)энциклопедия

В теории графов деревом называется связный граф без замкнутых путей (циклов).

Связность означает наличие путей между любой парой вершин, ацикличность — отсутствие циклов и то, что между парами вершин имеется только по одному пути.

Деревья удобно использовать для отображения иерархий, иерархического упорядочивания информации, для отображения последовательностей действий, организации вычислений и перебора, изображения схем алгоритмов без циклов, представления ходов игр.

Пример решения известной задачи про волка, козу и капусту:

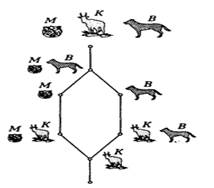
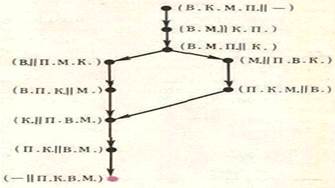
Подобная схема действий является ориентированным графом – таким, в котором рёбра являются однонаправленными стрелками. В этой задаче граф действий не является деревом. Однако его можно изобразить в виде дерева, если допускать существование вершин, кодирующих одинаковые ситуации, но отличающиеся по истории прихода к этим ситуациям. При таком способе кодирования количество листьев внизу даёт количество исходов задачи.

Ориентированное (направленное) дерево — ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями.

· Степень вершины — количество инцидентных ей ребер (пересекающихся в ней).

· Концевой узел (лист, терминальная вершина) — узел со степенью 1.

· Узел ветвления — неконцевой узел.

· Уровень узла — длина пути от корня до узла. Можно определить рекурсивно:

1. уровень корня дерева 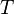равен 0;

2. уровень любого другого узла на единицу больше, чем уровень корня ближайшего поддерева дерева 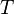, содержащего данный узел.

· Дерево с отмеченной вершиной называется корневым деревом.

· -й ярус дерева 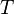— множество узлов дерева, на уровне от корня дерева.

· частичный порядок на вершинах: 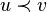, если вершины и 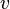различны и вершина лежит на (единственной!) элементарной цепи, соединяющей корень с вершиной .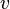

· корневое поддерево с корнем 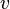— подграф .

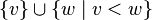· Дерево без выделенного корня называется свободным.

· Остовное дерево (остов) — это подграф графа, содержащий все его вершины и являющийся деревом. Рёбра графа, не входящие в остов, называются хордами графа относительно остова.

· Несводимым называется дерево, в котором нет вершин степени 2.

· Лес — множество (обычно упорядоченное), не содержащее ни одного непересекающегося дерева или содержащее несколько непересекающихся деревьев.

Дата добавления: 2015-10-13