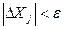Ітерації припиняють, коли задовольняється нерівність

(1.14)

Метод Ньютона гарантує збіжність тільки за таких умов:

1) на інтервалі пошуку кореня витримується (1.4), тобто функція y=y(x) монотонна;

2) на інтервалі пошуку кореня друга похідна не змінює знак:

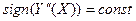, (1.15)

тобто функція y=y(x) не має точок перетину;

3) нульове наближення X₀ вибране так, що

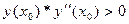. (1.16)

На рис. 9 зображено блок-схему алгоритму визначення кореня рівняння (1.1) за методом Ньютона. Тут також уведено лічильник циклу, щоб забезпечитися на випадок зациклення, якщо не витримуються умови збіжності чи у програмі допущена помилка.

Метод Ньютона на відміну від двох попередніх вимагає обчислення на кожній ітерації не тільки функції y = y(x) – лівої частини рівняння (1), але і похідної 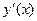. Ця похідна може обчислюватися за формулою, якщо функція диференціюється аналітично, або наближено чисельним методом.

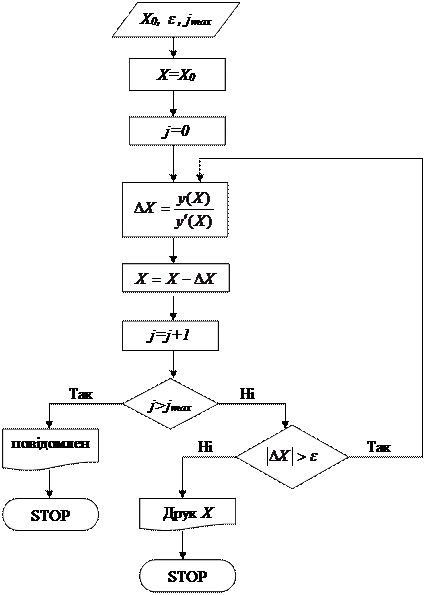
Рис.9. Блок-схема методу Ньютона

При складанні програми для обчислення y(x) та 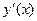можна задати підпрограми - функції.

Исходные данные:

а0 =1.25

а1 =0.07

а2 = 2.17

а3 =1.8

а4 =0.01

а5 =0.04

Ее =25 В

Re =10 Ом

Внешний вид экранной формы:

Внешний вид экранной формы состоит из четырех закладок, содержащих результаты расчетов.

Закладка «Общая часть»

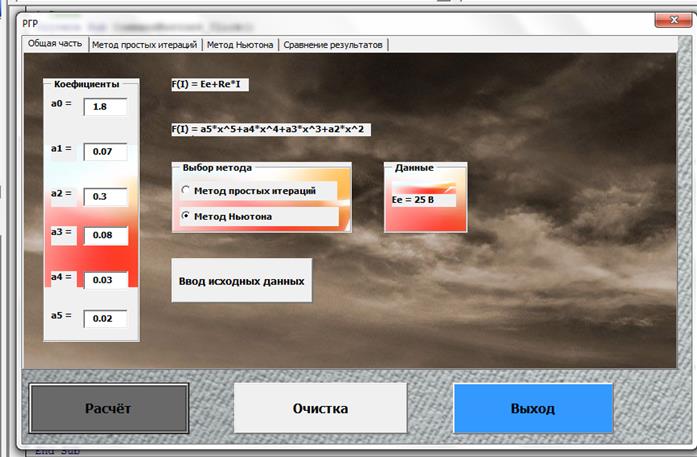
Закладка «Метод простых итераций»

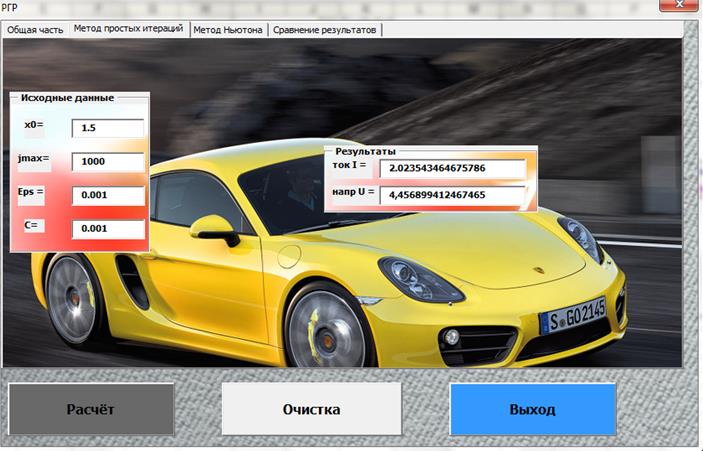
Закладка «Метод Ньютона»

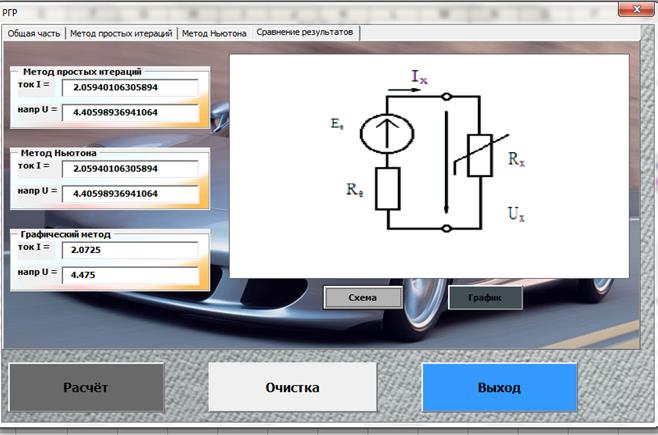
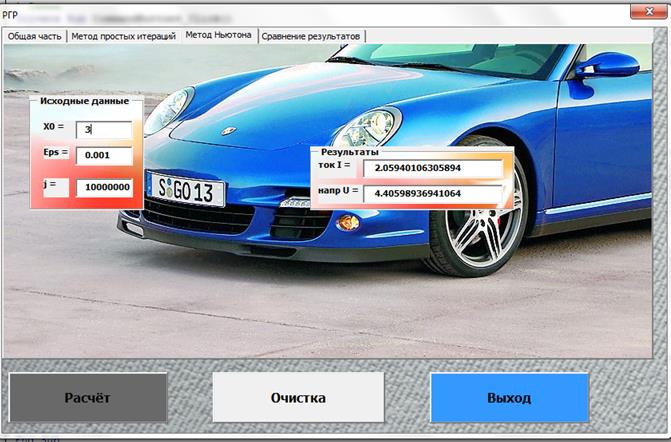Закладка «Сравнение результатов»

№	Назвние объекта	Имя	Название подпрограммы
	РГР Рожко Виталий	UserForm1	-----
	Общая часть	Page1	-----
	Метод половинного деления	Page2	-----
	Метод Простых итераций	Page3	-----
	Сравнение результатов	Page4	-----
	Значение коэффициентов	CommandButton1	Private Sub CommandButton1_Click()
	Расчет	CommandButton2	Private Sub CommandButton2_Click()
	Очистка	CommandButton3	Private Sub CommandButton3_Click()
	Выход	CommandButton4	Private Sub CommandButton4_Click()
	Схема	CommandButton5	Private Sub CommandButton5_Click()
	График	CommandButton6	Private Sub CommandButton6_Click()
	Метод половинного деления	OptionButton1	-----
	Метод Простых итераций	OptionButton2	-----
	Результат:	Frame1	-----
	Исходные данные:	Frame2	-----
	Метод расчёта:	Frame3	-----
	Половинного деления:	Frame4	-----
	Ньютона:	Frame5	-----
	Графический метод	Frame6	-----
	Исходные лданные:	Frame7	-----
	Погрешность:	Frame8	-----
	Результат:	Frame9	-----
	Значения:	Frame10	-----
	a0 =	Label 3	-----
	a1 =	Label 4	-----
	a2 =	Label 5	-----
	a3 =	Label 6	-----
	a4 =	Label 7	-----
	a5 =	Label 8	-----
	Ee =	Label 9	-----
	Re =	Label 10	-----
	x0 =	Label 18	-----
	jmax=	Label 19	-----
	Eps =	Label 20	-----
	C =	Label 21	-----
	а =	Label 12	-----
	b =	Label 13	-----
	j =	Label 16	-----
	Eps =	Label 14	-----
	I =	Label 15	-----
	U =	Label 16
	I =	Label 30
	U =	Label 31
	I =	Label 24
	U =	Label 25	-----
	I =	Label 26	-----
	U =	Label 27	-----
	I =	Label 28	-----
	U =	Label 29	-----
	Поле ввода	TextBox1	-----
	Поле ввода	TextBox2	-----
	Поле ввода	TextBox3	-----
	Поле ввода	TextBox4	-----
	Поле ввода	TextBox5	-----
	Поле ввода	TextBox6	-----
	Поле ввода	TextBox7	-----
	Поле ввода	TextBox8	-----
	Поле ввода	TextBox9	-----
	Поле ввода	TextBox10	-----
	Поле ввода	TextBox11	-----
	Поле ввода	TextBox12	-----
	Поле ввода	TextBox13	-----
	Поле ввода	TextBox14	-----
	Поле ввода	TextBox15	-----
	Поле ввода	TextBox16	-----
	Поле ввода	TextBox18	-----
	Поле ввода	TextBox19	-----
	Поле ввода	TextBox20	-----
	Поле ввода	TextBox21	-----
	Поле ввода	TextBox22	-----
	Поле ввода	TextBox23	-----
	Картинка	Image1	-----
	Картинка	Image2	-----

Тексты всех подпрограмм:

Dim a0, a1, a2, a3, a4, a5 As Single

Dim a, b, c, Eps, I, U, Fa, Fb, Fc As Double

Dim x0, jmax As Integer

' Объявление функции

Private Function F(x)

F = a5 * x ^ 5 + a4 * x ^ 4 + a3 * x ^ 3 + a2 * x ^ 2 + a1 * x + a0

End Function

' Объявление производной

Private Function Fpr(x)

Fpr = 5 * a5 * x ^ 4 + 4 * a4 * x ^ 3 + 3 * a3 * x ^ 2 + 2 * a2 * x + a1

End Function

' Ввод

Private Sub CommandButton1_Click()

TextBox1.Value = "1.8"

TextBox2.Value = "0.07"

TextBox3.Value = "0.3"

TextBox4.Value = "0.08"

TextBox5.Value = "0.03"

TextBox6.Value = "0.02"

TextBox7.Value = "1.5"

TextBox8.Value = "1000"

TextBox9.Value = "0.001"

TextBox12.Value = "3"

TextBox13.Value = "0.001"

TextBox14.Value = "10000000"

TextBox35.Value = "0.01"

End SubEnd Sub

' Расчёт

Private Sub CommandButton2_Click()

a = Val(TextBox10.Value)

b = Val(TextBox9.Value)

c = Val(TextBox17.Value)

Eps = Val(TextBox11.Value)

a0 = Val(TextBox1.Value)

a1 = Val(TextBox2.Value)

a2 = Val(TextBox3.Value)

a3 = Val(TextBox4.Value)

a4 = Val(TextBox5.Value)

a5 = Val(TextBox6.Value)

Eps = Val(TextBox16.Value)

jmax = Val(TextBox15.Value)

x0 = Val(TextBox14.Value)

Ee = 25

Re = 10

' простые итерации

If OptionButton1.Value = True Then

x = x0

j = 0

xn = c * F(x) + x0

j = 0

j = j + 1

If j > jmax Then

MsgBox "Достигнуто максимальное количество итераций"

GoTo Z1

If Abs(xn - x0) < Epsi Then

x = xn

Else

Z1: xn = c * F(x) + x0

End If

End If

U = Ee - Re * x

TextBox10.Value = Str(x)

TextBox11.Value = Str(U)

TextBox17.Value = Str(x)

TextBox18.Value = Str(U)

MsgBox (xn)

MsgBox (U)

End If

' метод Ньютона

If OptionButton2.Value = True Then

x = x0

j = 0

xn = c * F(x) + x0

For j = 0 To jmax

If j > jmax Then

MsgBox "fgh"

Else

If Abs(xn - x0) < Eps Then

x = xn

TextBox18.Text = Str(x)

TextBox22.Text = Str(x)

Else

TextBox18.Text = xn

TextBox22.Text = xn

End If

End If

Next j

U = Ee - Re * x

TextBox19.Text = Str(U)

TextBox23.Text = Str(U)

End If

End Sub

' Очистка

Private Sub CommandButton3_Click()

TextBox1.Value = ""

TextBox2.Value = ""

TextBox3.Value = ""

TextBox4.Value = ""

TextBox5.Value = ""

TextBox6.Value = ""

TextBox7.Value = ""

TextBox8.Value = ""

TextBox9.Value = ""

TextBox10.Value = ""

TextBox11.Value = ""

TextBox12.Value = ""

TextBox13.Value = ""

TextBox14.Value = ""

TextBox15.Value = ""

TextBox16.Value = ""

TextBox17.Value = ""

TextBox18.Value = ""

TextBox19.Value = ""

TextBox20.Value = ""

TextBox21.Value = ""

TextBox22.Value = ""

TextBox23.Value = ""

TextBox24.Value = ""

TextBox25.Value = ""

End Sub

' Выход

Private Sub CommandButton4_Click()

UserForm1.Hide

End Sub

' Схема

Private Sub CommandButton5_Click()

Image1.Visible = True

Image2.Visible = False

End Sub

' График

Private Sub CommandButton6_Click()

Image2.Visible = True

Image1.Visible = False

TextBox24.Value = "1.5"

TextBox25.Value = "10"

End Sub

Результаты графического решения нелинейного уравнения в Microsoft Excel:

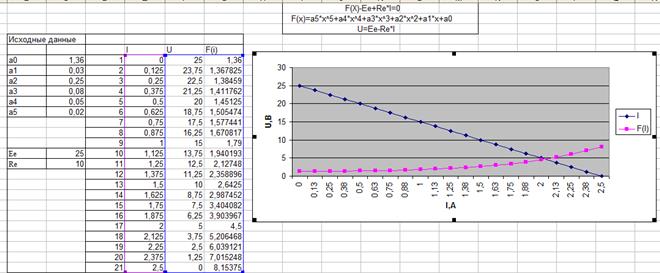
Вывод:

В расчётно-графической работе необходимо было рассчитать нелинейное уравнение тремя предложенными методами: метод половинного деления, метод простых итераций, графический метод. Выполнив расчёты по данным методам, оказалось, что самым легким и точным является графический метод решения.

Дата добавления: 2015-10-13