МДНФ логических функций.

Минимизацию логических функций проведем с помощью карт Карно.

При нахождении МДНФ данный метод отличается от того, как находили МКНФ, следующим. Сначала вместо лог. 0 выделяются лог. 1. Дизъюнкция заменяется конъюнкцией, и наоборот. Инвертируются те аргументы, значение которых равно лог. 0.

Y1:

X3X4   X1X2
01

Область	Набор значений аргументов
1 (с)
2 (к)	010*
3 (з)	*101
4 (ф)

МДНФ для функции Y1 имеет следующий вид:

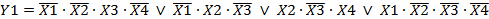
Y2:

X3X4   X1X2
11

Область	Набор значений аргументов
1 (к)	*0*1
2 (ф)	0*01
3 (з)	1*11

МДНФ для функции Y2 имеет следующий вид:

Y3:

X3X4   X1X2

Область	Набор значений аргументов

МДНФ для функции Y3 имеет следующий вид:

Представление логических функций в базисе ИЛИ-НЕ.

Представление логической функции в базисе ИЛИ-НЕ проведем с помощью МКНФ.

Сначала функция дважды инвертируется, а затем преобразуется с помощью формул де Моргана.

Дата добавления: 2015-10-13