Метод турбулентной диффузии

Этот метод разработан на основании использования турбулентной диффузии. Выполнив интегрирование дифференциального уравнения переноса водяного пара в турбулентной атмосфере по высоте от 0 до Ζ с учетом упрощений, получим:

ρ=((2.9)

Второе слагаемое в уравнении (2.9) представляет собой поток водяного пара при z =0, то есть испарение с водной поверхности. Обозначим его через Е, тогда уравнение примет вид:

Е = р * k * / , (2.10)

В формуле (2.10) выполним замену на е – парциальное давление водяного пара в воздухе согласно соотношению:

= 0,623 * е / (Р – 0,378 е), (2.11)

Е = р* k * 0,623/Р * 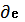/ , (2.12)

Изучая структуру турбулентного воздушного потока в приземном слое, А.Р. Константинов использовал следующее выражение для коэффициента турбулентного обмена при равновесной стратификации:

K = χ² * z * ω₁ / I_п (Z₁ / Z₀), (2.13),

где χ = 0,38 – постоянная Кармана;

Ζ – высота измерения;

Z₀ – высота шероховатости, то есть уровень, на котором скорость ветра равна 0; ω1 – скорость ветра на высоте Z₁ = 1 метр.

Подставив выражение (2.13) в уравнение (2.12), и проинтегрировав его с учетом логарифмического закона распределения парциального давления водяного пара по высоте. Получим выражение для расчета испарения в общем виде:

Е = b * ω₁ *(е_о –е₂), (2.14)

Подставив в него средние значения метеорологических элементов, получим

Е = 0,12 * ω₁ *(е_о - е₂), (2.15),

где Е – слой испарившейся воды, мм/сутки.

2.5. Расчёт испарения по эмпирическим формулам

В наше время разработано большое число эмпирических формул для расчета испарения, но почти все они имеют структуру, предложенную ещë Дальтоном в 1802 г.:

Е = ε₀ *(е_о –е₂), (2.16),

где ε₀ – коэффициент, зависящий от скорости ветра.

Авторами формул определения коэффициента ɛ₀ являются: Л.Г. Карпентер, Д.И. Бибиков, Б.В. Проскуряков, А.Р. Константинов. А.П. Блаславский и др.

Наибольшее распространение получила формула В.Д. Зайкова:

ε₀ = 0,15 (1+ 0,72 ω₂), (2.17),

где ω₂ – скорость ветра на высоте 2 м над поверхностью воды.

Т.о. подставляя (2.17) в (2.16) получаем формулу:

Е = 0,15 (1+ 0,72 ω₂) * (е_о –е₂). (2.18),

где Е – слой испарившейся воды, мм/сут;

е_о и е₂ – давление насыщенного водяного пара и парциальное давление водяного пара, гПа;

ω₂ – скорость ветра. м/с.

Проверка точности различных формул по оценке испарения с водной поверхности, проведенная в Государственном гидрологическом институте, показала, что наиболее оптимальной является формула:

Е = 0,14 (1+ 0,72 ω₂) * (е_о –е₂), (2.19)

Эта формула была названа формулой ГГИ. Она применяется для водоемов, расположенных на равнинной территории и в условиях равновесной стратификации, т.е. когда разность значений температуры воды и воздуха не превышает 4°С. При наличии данных гидрометеорологических наблюдений расчет испарения по формуле ГГИ не представляет каких-либо затруднений. Для расчета испарения при отсутствии данных необходимы следующие сведения:

· местоположение, конфигурация, площадь, глубина и характер защищенности водоëма;

· средние за расчетный интервал времени значения температуры, абсолютной влажности воздуха. Скорости ветра и распределения его по направлениям, общей и нижней облачности по данным ближайшей к водоему метеостанции;

· характеристика местоположения метеостанции, степень еë защищенности от ветра и рельеф в районе станции.

Значения испарения, вычисленные по формулам различных авторов при штилевой обстановке значительно различаются. Это объясняется тем, что при штиле на испарение существенное воздействие оказывает вертикальный конвективный воздухообмен над испаряющей поверхностью. Чем больше разность температуры испаряющей поверхности и воздуха, тем интенсивнее протекает воздухообмен, а следовательно, и более интенсивно осуществляется отвод паров от водной поверхности в вышерасположенные слои. Проведенные в 60-х годах исследования показали, что интенсивность испарения прямо пропорциональна разности температуры воды и воздуха не только при полном штиле, но и при слабом ветре. Поэтому формула ГГИ была уточнена введением ещë одного слагаемого, зависящего от разности температуры испаряющей поверхности воды и воздуха на высоте 2 м. Введением этой характеристики учитывается скорость отвода водяных паров от испаряющей поверхности в атмосферу. Эти формулы имеют следующий вид:

формула В.А. Рымши и Р.В. Донченко

Е = 0,14 (k₁+ 0,72 ω₂) * (е_о –е₂), (2.20),

где k₁ – коэффициент, зависящий от разности температуры поверхности воды и воздуха на высоте 2 м (t_п – θ₂), определяется по таблице;

формула Л.Г. Шуляковского

= * (е_о –е₂), (2.21)

формула А.Р. Константинова

Е = 0,024 * (t_п – θ₂) / ω₁ + 0,116 ω₁) * (е_о –е₂), (2.22)

формула А.П. Блаславского и С.Н. Нургалиева

= 0,14 * * (е_о –е₂), (2.23),

k₂ – коэффициент, зависящий от разности температуры поверхности воды и воздуха на высоте (t_п – θ₂), определяется по таблице.

Эта формула наиболее часто используется для расчета термического режима водохранилищ.

Формула Н.Н. Иванова является эмпирической формулой другого типа:

Е = 0,0018 * (25 + θ₂)² * (100 – r₂), (2.24),

где Е – слой испарившейся воды, мм/мес;

θ₂ и r ₂ – средние месячные температура и относительная влажность воздуха.

Однако формула Иванова дает менее точные значения испарения, поэтому формула может применяться только в приближенных расчетах.

Существует также формула В.И. Бабкина, которую также можно отнести к эмпирическим формулам:

Е = Е_о * Δ / , (2.25),

где Е_о – максимальная скорость испарения;

– параметр, определяемый по графику;

δ – коэффициент турбулентного обмена;

h – высота, на которой измеряется парциальное давление водяного пара e;

R – газовая постоянная, отнесённая к 1 молю;

Т – абсолютная температура воды;

– относительная молекулярная масса;

Чтобы рассчитать испарение по приведенным выше формулам, используют данные о состоянии воздушной массы, полученные на континентальных метеостанциях, но с учетом еë трансформации при переходе с суши на водную поверхность. Для корректировки данных континентальных метеостанций, их корректируют введением коэффициентов:

1. Скорость ветра на высоте 2 м над поверхностью водоема ɷ₂ корректируется введением сразу трех поправочных коэффициентов, т.е.:

ω₂ = k₁ * k₂ * k₃ * , (2.26),

где k₁, k₂, k₃ – коэффициенты, учитывающие соответственно степень защищенности метеорологической станции на суше, характер рельефа в пункте наблюдений и среднюю длину разгона воздушного потока над водной поверхностью водоëма;

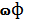– скорость ветра на высоте флюгера.

2. Парционное давление водяного пара на высоте 2 м над поверхностью водоëма рассчитывается следующим образом:

е₂ = е _'2 + (0,8 е₀ – е _'2) * М, (2.27),

где е_'2 – парциальное давление водяного пара, измеренное на высоте 2 м на континентальной метеостанции;

е₀ – давление насыщенного водяного пара, определенное по температуре поверхности воды;

М – коэффициент трансформации, учитывающий изменение влажности и температуры воздуха в зависимости от размера водоема.

3. Температура воздуха на высоте 2 м над поверхностью водоëма уточняется аналогично парциальному давлению водяного пара:

θ₂ = θ_'2 + (t_п - θ_'2), * м, (2.28),

где θ_'2 – температура воздуха на высоте 2 м на континентальной метеостанции;

t_п – температура поверхности воды.

3. Расчёт характеристики

Дата добавления: 2015-09-07