
Кафедра ЭВМ
Курсовая работа
по курсу: «СИСТЕМЫ АНАЛОГОВЫХ КОМПОНЕНТОВ КОМПЬЮТЕРНЫХ СИСТЕМ»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ТЕМА: «ИССЛЕДОВАНИЕ ФИЛЬТРУЮЩИХ ЭЛЕМЕНТОВ ФНЧ БАТТЕРВОРТА И ЧЕБЫШЕВА»
Руководитель ……………………………………………………..
(подпись, дата, должность, фамилия и инициалы)
Студент …………………………………………………………….
(подпись, дата, группа, фамилия и инициалы)
Харьков 2011
ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ РАДИОЭЛЕКТРОНИКИ
(наименование высшего учебного заведения)
| Кафедра: | Электронно-вычислительных машин | ||||
| Дисциплина: | Схемотехника аналоговых компонентов компьютерных систем | ||||
| Специальность: | Компьютерные системы и сети | ||||
| Курс: | 3й. | Группа: | КИ-09-1 | Семестр: | 5й |
З А Д А Н И Е
на курсовой проект (работу) студента
Михайлова Любовь Олеговна.
(фамилия, имя, отчество)
| 1. Тема проекта (работы) Провести исследование фильтрующих элементов ФНЧ Баттерворта и Чебышева (1дБ), fср=20кГц. | |||
| 2. Срок сдачи студентом законченного проекта (работы) | |||
| 3. Исходные данные к проекту (работе) | |||
| 4. Содержание пояснительной записки (перечень подлежащих разработке вопросов): | |||
| 5. Перечень графического материала (с точным указанием обязательных чертежей): | |||
| 6. Дата выдачи задания: | |||
КАЛЕНДАРНЫЙ ЛИСТ
| № п/п | Наименование этапов курсового проекта (работы) | Срок выполнения этапов проекта (работы) | Примечание |
| Студент | |||||
| (подпись) | |||||
| Руководитель | (подпись) | (фамилия, имя, отчество) | |||
| «» | 20__г. | ||||
Реферат
Пояснительная записка содержит в себе 20 страниц и 13 иллюстраций.
Предметом исследовании является фильтрующий элемент, а именно фильтры нижних частот Баттерворта и Чебышева при частоте среза fср=20кГц и неравномерностью А=1 дБ.
Целью исследования является закрепление знаний, полученных в курсе «Схемотехника аналоговых компьютеров компьютерных систем», овладение методами расчёта фильтров нижних частот и программного моделирования фильтров.
Методом решения задачи является моделирование схем заданных фильтров нижних частот Баттерворта и Чебышева с использованием среды Multisim 11.0 пакета National Instruments.
В результате исследования были получены графики, иллюстрирующие амплитудно-частотные характеристики построенных в работе фильтров.
КЛЮЧЕВЫЕ СЛОВА: ФИЛЬТР НИЗКИХ ЧАСТОТ (ФНЧ), ФИЛЬТР БАТТЕРВОРТА, ФИЛЬТР ЧЕБЫШЕВА, ЧАСТОТА СРЕЗА, СПЕКТР ПРОПУСКАНИЯ, ПОРЯДОК ФИЛЬТРА.
СОДЕРЖАНИЕ
Введение....……………………………………………………………………...6
1. Теоретическая часть.…………………………………………………………..7
1.1 Общие сведения о фильтрах нижних частот…….………………………7
1.2 Фильтр нижних частот Баттерворта………………………………………8
1.3 Фильтр нижних частот Чебышева………………………………………...9
2. Правила расчёта фильтров нижних частот………………………………....11
2.1 Общие правила расчёта фильтров нижних частот……………………..11
2.2 Фильтр нижних частот Баттерворта……………………………………12
2.3 Фильтр нижних частот Чебышева…………………………………….....13
3. Моделирование фильтров нижних частот…………………………………16
3.1 Фильтр нижних частот Баттерворта……………………………………16
3.2 Фильтр нижних частот Чебышева……………………………………....17
Выводы………………………………………………………………………...19
Перечень используемых источников………………………………………..20
ВВЕДЕНИЕ
Во многих радиотехнических устройствах часто возникает необходимость выделения заданных частотных диапазонов из имеющегося спектра частот. Выделение требуемой полосы частот с очень малым затуханием осуществляется фильтрами. Одними из самым часто используемых являются электрические фильтры.
В большинстве случаев электрический фильтр представляет собой частотно-избирательное устройство. Следовательно, он пропускает сигналы определенных частот и задерживает или ослабляет сигналы других частот.
Наиболее общими типами частотно-избирательных фильтров являются:
1) фильтры нижних частот – пропускают низкие частоты и задерживают высокие частоты,
2) фильтры верхних частот – пропускают высокие частоты и задерживают низкие частоты,
3) полосно-пропускающие фильтры – пропускают полосу частот и задерживают те частоты, которые расположены выше и ниже этой полосы,
4) полосно-заграждающие фильтры – задерживают полосу частот и пропускают частоты, расположенные выше и ниже этой полосы.
Благодаря применению электрических фильтров оказалось возможным осуществление многих магистралей дальней телефонной, телеграфной и других видов связи.
1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1.1 ОБЩИЕ СВЕДЕНИЯ О ФИЛЬТРАХ НИЖНИХ ЧАСТОТ
Фильтр нижних частот (ФНЧ) – один из видов аналоговых или электронных фильтров, эффективно пропускающий частотный спектр сигнала ниже некоторой частоты (частоты среза), и уменьшающий (подавляющий) частоты сигнала выше этой частоты. Степень подавления каждой частоты зависит от вида фильтра.
Фильтры нижних частот без искажения передают сигналы нижних частот.
В начале нашего столетия ФНЧ, составленные из ряда катушек индуктивности (сопротивлений) и конденсаторов, получили широкое применение в технике.
Известный интерес представляют пассивные цепочные, или лестничные фильтры, состоящие из комбинаций элементов L ® и C и не требующие источника питания. Пассивные фильтры могут обладать как широкими полосами пропускания, так и очень узкими.

Рис. 1.1.1 – Простой фильтр нижних частот
В общем случае определяется полоса пропускания как интервал частот 0<w<wс, полоса задерживания как частоты w>w1 и переходная область как диапазон частот wc<w<w1 (wc – частота среза). Эти частоты обозначены на рис. 1.1.2, на котором приведена реальная амплитудно-частотная характеристика фильтра нижних частот, где в данном случае заштрихованные области представляют собой допустимые отклонения характеристики в полосах пропускания и задерживания.

Рис. 1.1.2 – Реальная амплитудно-частотная характеристика ФНЧ
Невозможно создать идеальные фильтры, но с помощью реализуемых фильтров (которые разрабатываются на основе реальных схемных элементов (рис.1.1.3)) можно получить приближения к идеальным. Передаточная функция реализуемого фильтра представляет собой отношение полиномов. Степень полинома знаменателя n определяет порядок фильтра. Практика показывает, что реальные амплитудно-частотные характеристики лучше для фильтров более высокого порядка. Таким образом, один из аспектов разработки фильтров связан с получением реализуемой характеристики, аппроксимирующей с некоторой заданной степенью точности идеальную характеристику при наименьших затратах.

Рис. 1.1.3 – Реализация ФНЧ с помощью ОУ
1.2 ФИЛЬТР НИЖНИХ ЧАСТОТ БАТТЕРВОРТА
Фильтр Баттерворта — один из типов электронных фильтров. Фильтры этого класса отличаются от других методом проектирования. Фильтр Баттерворта проектируется так, чтобы его амплитудная частотная характеристика была максимально гладкой на частотах полосы пропускания.
В радиотехнике и связи фильтры Баттерворта используются потому, что их частотная характеристика близка к прямоугольной, что позволяет осуществлять избирательный прием сигналов от разных радиостанций. Чем выше порядок фильтра, тем лучше избирательность.
Схема активного фильтра Баттерворта на частоту 20 кГц, показанная на рис.1.2.1, предотвращает наложение спектров и ограничивает частотный диапазон в аудиосистемах.

Рис. 1.2.1 – ФНЧ Баттерворта
АЧХ фильтра нижних частот Баттерворта максимально гладкая на частотах полосы пропускания и снижается практически до нуля на частотах полосы подавления (рис. 1.2.2). В случае фильтра первого порядка АЧХ затухает со скоростью −6 децибел на октаву (-20 децибел на декаду) (на самом деле все фильтры первого порядка независимо от типа идентичны и имеют одинаковый частотный отклик). Для фильтра Баттерворта второго порядка АЧХ затухает на −12 дБ на октаву, для фильтра третьего порядка — на −18 дБ и так далее. АЧХ фильтра Баттерворта — монотонно убывающая функция частоты.

Рис. 1.2.2 – АЧХ ФНЧ Баттерворта
Фильтр Баттерворта — единственный из фильтров, сохраняющий форму АЧХ для более высоких порядков (за исключением более крутого спада характеристики на полосе подавления), тогда как многие другие разновидности фильтров (фильтр Бесселя, фильтр Чебышева, эллиптический фильтр) имеют различные формы АЧХ при различных порядках.
1.3 ФИЛЬТР НИЖНИХ ЧАСТОТ ЧЕБЫШЕВА
Фильтр Чебышева – один из типов линейных аналоговых или цифровых фильтров, отличительной особенностью которого является более крутой спад амплитудно-частотной характеристики (АЧХ) и существенные пульсации амплитудно-частотной характеристики на частотах полос пропускания (фильтр Чебышёва I рода) и подавления (фильтр Чебышёва II рода), чем у фильтров других типов. Фильтр получил название в честь известного русского математи- А XIX века Пафнутия Львовича Чебышева, так как характеристики этого фильтра основываются на многочленах Чебышева.
Фильтры Чебышева обычно используются там, где требуется с помощью фильтра небольшого порядка обеспечить требуемые характеристики АЧХ, в частности, хорошее подавление частот из полосы подавления, и при этом гладкость АЧХ на частотах полос пропускания и подавления не столь важна.

Рис. 1.3.1 – простейший ФНЧ Чебышева на пассивных элементах
Характеристика фильтра Чебышева спадает более круто за частотой среза (рис. 1.3.2). В полосе пропускания она имеет волнообразный характер с постоянной амплитудой. При задании порядка фильтра более резкому спаду амплитудно-частотной характеристики соответствует большая неравномерность в полосе пропускания.

Рис. 1.3.2 – АЧХ ФНЧ Чебышева
Следует так же упомянуть такую величину, как критерий приближения Чебышева, который широко используется не только в теории фильтров – минимум максимальной ошибки приближения (минимаксное приближение). В соответствии с этим приближением параметры передаточной функции подбираются таким образом, чтобы в полосе передачи АЧХ наблюдались равноволновые пульсации коэффициента передачи, которые являются «платой» за повышение крутизны среза фильтра.
2 ПРАВИЛА РАСЧЁТА ФИЛЬТРОВ НИЖНИХ ЧАСТОТ
2.1 ОБЩИЕ ПРАВИЛА РАСЧЁТА ФИЛЬТРОВ НИЖНИХ ЧИСТОТ





 ;
;
 Положив:
Положив: 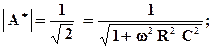
получим частоту среза  Фазовый сдвиг на этой частоте – 450.
Фазовый сдвиг на этой частоте – 450.

 заменим на
заменим на  .
.
Передаточная функция фильтра:

 Передаточная функция определяет зависимость преобразований Лапласа выходного и входного напряжений для произвольных временных сигналов. Переход от передаточной функции
Передаточная функция определяет зависимость преобразований Лапласа выходного и входного напряжений для произвольных временных сигналов. Переход от передаточной функции  к частотной характеристики
к частотной характеристики  для синусоидальных входных сигналов можно выполнить, положив
для синусоидальных входных сигналов можно выполнить, положив 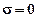 .
.
 Нормированная комплексная переменная:
Нормированная комплексная переменная:
 при
при 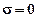

Частота среза фильтра 
Тогда 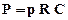

 при W >> 1; т.е. f >>fg
при W >> 1; т.е. f >>fg
 это соответствует снижению коэффициента передачи фильтра 20дБ / декаду.
это соответствует снижению коэффициента передачи фильтра 20дБ / декаду.
Для последовательно включенных n фильтров нижних частот:
 .
.
Где a1, a2….. an - действительные положительные коэффициенты.
 при W >> 1.
при W >> 1.
Уменьшение коэффициента передачи характеризуется величиной n × 20дБ на каждую декаду. Корни передаточной функции являются отрицательными и действительными. Такими свойствами обладают пассивные RC фильтры n – ного порядка.
В общем, виде передаточная функция фильтра нижних частот:
 (2.1.1)
(2.1.1)
где c1, c2,×××× cn – положительные действительные коэффициенты.
Порядок фильтра определяется максимальной степенью переменной Р.
Для реализации фильтра необходимо разложить полином знаменателя на множители. Если среди корней полинома есть комплексные, то в этом случае вместо этого представления следует записать в виде произведения сомножителей второго порядка.
 (2.1.2)
(2.1.2)
где ai и bi – положительные действительные коэффициенты. Для нечетных порядков полинома bi = 0.
2.2 ФИЛЬТР НИЖНИХ ЧАСТОТ БАТТЕРВОРТА
Модуль  .
.
График функции | А* |2 должен быть по возможности горизонтальным на частотах входного сигнала, меньше частоты среза. Т.к. в этой области W < 1, необходимо, чтобы функция | А* |2 зависела только от старшей степени W.
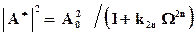 .(2.2.1)
.(2.2.1)
Коэффициент К2n определяется из условий нормировки, связанного с необходимостью обеспечения снижения коэффициента передачи фильтра на 3дБ при частоте среза W = 1.
 откуда К2n = 1.
откуда К2n = 1.
Тогда для фильтра Баттерворта n – ного порядка выражение имеет следующий вид:
 (2.2.2)
(2.2.2)
Для расчета | А* | необходимо знать соответствующий выражению (2.2.2) комплексный коэффициент передачи.

| n | Полином Баттерворта |
| 1 + Р | |

| |

| |

|
Аналитические выражения для коэффициентов аi и bi передаточной функции (1.1.2) для фильтра Баттерворта.
Коэффициенты ai и bi:
для четных n

bi = 1.
Для нечетных n
а1 = 1 b1 = 0


 bi = 1
bi = 1
2.3 ФИЛЬТР НИЖНИХ ЧАСТОТ ЧЕБЫШЕВА
Характеристика фильтра Чебышева спадает более круто за частотой среза. В полосе пропускания она имеет волнообразный характер с постоянной амплитудой. При задании порядка фильтра более резкому спаду амплитудно-частотной характеристики соответствует большая неравномерность в полосе пропускания.

В области  функция
функция  колеблется между 0 и 1, а при Х > 1 монотонно возрастает.
колеблется между 0 и 1, а при Х > 1 монотонно возрастает.
| N | Полиномы Чебышева |

| |

| |

| |

|
Выражение для фильтров нижних частот на основе полиномов Чебышева:

Постоянный коэффициент k выбирается так, чтобы при Х = 0 выполнялось условие 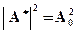 , т.е. k = 1 для полиномов нечетного порядка; k= 1 + e2 для четных n. Множитель e определяет степень неравномерности характеристики фильтра..
, т.е. k = 1 для полиномов нечетного порядка; k= 1 + e2 для четных n. Множитель e определяет степень неравномерности характеристики фильтра..

Отсюда 

| Неравномерность дБ | ||||
| 0,5 | ||||

| 1,059 | 1,122 | 1,1259 | 1,413 |
| К | 1,122 | 1,259 | 1,585 | 1,935 |
| e | 0,349 | 0,509 | 0,765 | 0,998 |
Однако, удобно вычислять полюсы передаточной функции фильтра непосредственно по:
 ;
;
и используя выражение для коэффициентов Баттерворта. Объединяя комплексно сопряженные полюсы передаточной функции для коэффициентов аi и bi:
Для четных n

для нечетных n:

 b/I = 0
b/I = 0
a/I = 1/ sh g

где 
подставив а/i; b/i вместо аi и bi в выражение

получим передаточную функцию фильтра Чебышева нижних частот, в котором Р нормировано не относительно wg (соответствующую коэффициенту передачи 3дБ), а относительно wс – при котором коэффициент передачи в последний раз принимает значение Аmin. После заменим Р на aР, и выберем постоянную нормирования a так, чтобы коэффициент передачи P = j имел значение  ; тогда
; тогда 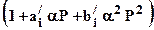 , где
, где  ;
;  . Коэффициенты для аi и bi передаточных функций для фильтров до 5 порядка для значений неравномерности АЧХ равных 0,5; 1; 2; 3дБ приведены в таблице 2.3.1.
. Коэффициенты для аi и bi передаточных функций для фильтров до 5 порядка для значений неравномерности АЧХ равных 0,5; 1; 2; 3дБ приведены в таблице 2.3.1.
Таблица 2.3.1 Коэффициенты для расчётов ФНЧ.
| N | аi | Bi | 
| Qi |
| Фильтр Баттерворта | ||||
| 1,0000 | 0,0000 | 1,000 | - | |
| 1,4142 | 1,0000 | 1,000 | 0,71 | |
| 1,000 | 0,0000 | 1,000 | - | |
| 1,0000 | 1,0000 | 1,272 | 1,00 | |
| 1,8478 | 1,0000 | 0,719 | 0,54 | |
| 0,7654 | 1,0000 | 1,390 | 1,31 | |
| 1,0000 | 0,0000 | 1,000 | - | |
| 1,6180 | 1,0000 | 0,859 | 0,62 | |
| 0,6180 | 1,0000 | 1,448 | 1,62 | |
| Фильтр Чебышева с неравномерностью 1дБ | ||||
| 1,0000 | 0,0000 | 1,000 | - | |
| 1,3022 | 1,5515 | 1,000 | 0,96 | |
| 2,2156 | 0,0000 | 0,451 | - | |
| 0,5442 | 1,2057 | 1,363 | 2,02 | |
| 2,5904 | 4,1601 | 0,540 | 0,78 | |
| 0,3039 | 1,1697 | 1,417 | 3,56 | |
| 3,5711 | 0,0000 | 0,280 | - | |
| 1,1280 | 2,4896 | 0,894 | 1,40 | |
| 0,1872 | 1,0814 | 1,486 | 5,56 |
3 МОДЕЛИРОВАНИЕ ФИЛЬТРОВ НИЖНИХ ЧАСТОТ
3.1 ФИЛЬТР НИЖНИХ ЧАСТОТ БАТТЕРВОРТА
Исследование ФНЧ Баттерворта проведём по схеме с рис.1.2.1
Выберем следующие параметры схемы:
R1=1.2 kOm;
R2=R3=2.5 kOm;
C1=C3=0.0078 uF;
C2=0.001 uF.

Рис.3.1.1 – Модель ФНЧ Баттерворта на ОУ
Используя блок body plotter снимем АЧХ вида:

Рис. 3.1.2 – АЧХ ФНЧ Баттерворта при fср=20кГц и А=1 дБ

Рис. 3.1.3 – идеальная АЧХ для ФНЧ Баттерворта
Так, как полученная экспериментальным путем АЧХ подобная идеальной АЧХ для ФНЧ Баттерворта, изображенной на рисунке 3.1.3, то параметры схемы были расчитаны верно.
3.2 ФИЛЬТР НИЖНИХ ЧАСТОТ ЧЕБЫШЕВА
Исследование ФНЧ Чебышева проведём по схеме 3.2.1.
Выберем следующие параметры схемы:
R1=13 kOm;
R2=11 kOm;
R3=6 kOm;
C1=0.007 uF;
C2=0.001 uF.

Рис.3.2.1 – Модель ФНЧ Чебышева
Используя блок body plotter снимем АЧХ вида:

Рис. 3.2.2 – АЧХ ФНЧ Чебышева при fср=20кГц и А=1 дБ
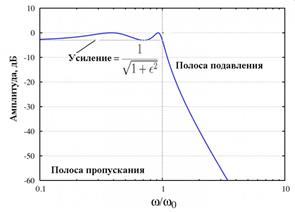
Рис. 3.2.3 – идеальная АЧХ для ФНЧ Чебышева
Так, как полученная экспериментальным путем АЧХ подобная идеальной АЧХ для ФНЧ Чебышева, изображенной на рисунке 3.2.3, то параметры схемы были расчитаны верно.
ВЫВОДЫ
В результате выполнения курсового проектирования по предмету «Схемотехника аналоговых компонентов компьютерных систем» были рассмотрены следующие вопросы:
- фильтры нижних частот (ФНЧ) и их назначение;
- основные сведения об ФНЧ Баттерворта и Чебышева;
- порядок расчёта ФНЧ Баттерворта и Чебышева.
Было выполнено моделирование вышеназванных фильтров нижних частот. Как для моделирования ФНЧ Баттерворта, так и для моделирования ФНЧ Чебышева использовались схемы на операционном усилителе.
В результате моделирования были сняты амплитудно-частотные характеристики фильтров, которые близки к идеальным характеристикам, описывающим каждый из видов исследуемых фильтров.
На основании полученных результатов можно предположить, что проектирование было выполнено успешно.
ПЕРЕЧЕНЬ ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
1. Титце У., Шенк К. Полупроводниковая схемотехника: Справочное руководство. - М.: Мир, 1982. – 512 с.
2. Справочник по активным фильтрамЖ Пер.с англ../Д.Джонсон, Дж.Джонсон, Г.Мур. – М.: Энергоатоммиздат, 1983 – 128 с.
3. Карлащук В.И. Электронная лаборатория на IBM PC. Программа Electronics Workbench и её преминение. – М.; Салон-Р, 1999, 506 с.
4. Методические указания по курсу «Схемотехника аналоговых».Раздел «Фильтры». Для студентов заочной формы обучения. – Харьков, 2003 – 33 с.
Дата добавления: 2015-09-07; просмотров: 118 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| На этом мы прощаемся с вами и до завтра. | | | Гривкова Екатерина. 1 страница |