Товары Х и Y называются субститутами, если они

а) состоят из одной и той же субстанции;

б) + могут заменять друг друга в потреблении;

в) имеют одинаковую предельную полезность для потребителя;

г) имеют одинаковую цену;

д) не продаются отдельно друг от друга.

8. Долгосрочный период – это период, в течение которого

а) конкуренция сменяется монополией;

б) убывающая отдача от масштаба обязательно сменяется возрастающей;

в) переменные издержки сокращаются до минимума;

г) + производитель может изменять объемы всех факторов производства;

д) + не существует разделения издержек на постоянные и переменные.

Оптимальная комбинация ресурсов может быть достигнута при условии, что

а) обеспечивается максимум продукции на минимум затрат;

б) выручка равна издержкам;

в) издержки равны нулю;

г) + обеспечивается максимальный выпуск при заданных издержках;

д) + минимизируются издержки при заданном выпуске.

В условиях чистой конкуренции предельный доход отдельной фирмы равен

а) + среднему доходу;

б) прибыли от реализации одной единицы продукции;

в) средней прибыли;

г) + рыночной цене единицы продукции;

д) нулю.

Ответы на вопросы 7 – 10 прямо формулируются в учебниках.

Всего за три части теста 60 баллов.

Задачи

(1) Долгое время на рынке клюковалок, продукта традиционного народного промысла, существовали следующие функции спроса и предложения: Q_d = 120 – P; Q_s = 0,5 P. Все покупатели имели идентичные индивидуальные функции спроса. К сожалению, в настоящее время половина покупателей ушла с рынка, в результате чего традиционный народный промысел приходит в упадок. Правительство рассматривает следующие два варианта стимулирования спроса для того, чтобы принять один из них:

1) введение для покупателей субсидии в процентах от цены единицы товара;

2) введение для покупателей потоварной субсидии.

Каким должен быть размер той и другой субсидии для того, чтобы восстановить прежний равновесный объем спроса? Каким должен быть общий размер той и другой субсидии в расчете на всех покупателей, вместе взятых?

Решение

Простой расчет показывает, что первоначально равновесная цена была равна 80, а равновесный объем 40. Очевидно, после ухода половины покупателей функция спроса будет иметь следующий вид: Q_d = 60 – 0,5 P. Рассмотрим оба варианта субсидии.

1) Предположим, для покупателей введена субсидия в виде доли х от цены товара. Тогда новая функция спроса изменится следующим образом: Q_d = 60 – 0,5(P – Рх). График этой функции должен проходить через точку, обозначающую прежний уровень равновесия (Р = 80; Q = 40). 40 = 60 – 0,5(80 – 80 х). Отсюда х = 0,5. Общий размер субсидии: 80Í 0,5 Í 40 = 1600.

2) Предположим, для покупателей введена потоварная субсидия в размере s. Тогда новая функция спроса изменится следующим образом: Q_d = 60 – 0,5 (P – s). График этой функции так же должен проходить через точку, обозначающую прежний уровень равновесия (Р = 80; Q = 40). 40 = 60 – 0,5 (80 – s). Отсюда s = 40. Общий размер субсидии: 40 Í 40 = 1600.

Ответ: 1) субсидия в процентах от цены товара должна быть равна 50%, общий размер субсидии 1600; 2) потоварная субсидия должна быть равна 40, общий размер субсидии 1600. (20 баллов)

(2) Два предпринимателя напилили и нарубили машину дров, причем длина каждого полена была равна 1 метру, после чего поехали продавать эти дрова в Китай. Как оказалось, такие длинные дрова в Китае не пользуются спросом, так как не помещаются ни в одну китайскую печку. Максимальная длина полена, которое можно продать, должна быть не больше 0,8 м. Поэтому предприниматели решили распилить каждое полено на две части.

Китайские коллеги, также торгующие дровами, любезно сообщили им следующую информацию. Оказывается, рыночная цена полена в общем и целом подчиняется простой закономерности: P = L^F, где L – длина полена в метрах (0 £ L £ 0,8). Проблема только в том, что показатель степени F точно не известен. А его величина определяет, на какие отрезки вы будете распиливать ваши сверхдлинные поленья для того, чтобы максимизировать суммарную рыночную цену двух полученных отрезков.

Определите, на какие два отрезка распилят каждое полено предприниматели в случае, если: 1) F > 1; 2) 0 < F < 1.

Решение (предложил Михаил Рыжих)

Предположим, мы распилили полено на два отрезка: х и (1 – х). Тогда их суммарная рыночная цена будет равна: Р = x ^F + (1 – x) ^F. P' = Fx ^{F- 1} – F (1 – x) ^{F- 1} = 0. x = 1 – x. Таким образом, максимум или минимум цены достигается при х = 0,5. Это значение х мы получили не случайно. Оно указывает на единственное в своем роде значение функции P = x ^F + (1 – x) ^F. Все остальные значения являются парными. Например, если мы отпилили от полена отрезок х = 0,4, то длина второго отрезка будет равна 0,6. А если мы отпилим отрезок, равный 0,6, то длина второго отрезка будет 0,4. Совершенно очевидно, что в обоих этих случаях значение Р будет одинаковым – правда, мы пока еще не знаем, каким именно – больше или меньше, чем значение Р при х = 0,5. Одинаковыми будут значения P и на границах интервала возможных значений х (0,2 < x < 0,8).

Учитывая это, рассмотрим первый случай, когда F > 1. Для того чтобы определить, что мы имеем – максимум или минимум – при х = 0,5, определим знак производной P' при х = 0,2 и х = 0,8. Знак производной P' = Fx ^{F- 1} – F (1 – x) ^{F- 1} равен знаку величины [ x ^{F- 1} – (1 – x) ^{F- 1} ]. Очевидно, при F > 1 и х = 0,2 выполняется: 0,2 ^{F -1} – 0,8 ^{F -1} < 0. P' < 0. Так же легко можно доказать, что при х = 0,8 P' > 0. Это значит, что при F > 1 и х = 0,5 достигается минимум функции Р. А максимум Р мы обеспечим, если выберем значения х на границах интервала (0,2; 0,8). То есть при F > 1 полено распиливается на две части: 0,2 м и 0,8 м.

Аналогично можно доказать, что при F Î (0; 1) полено распиливается пополам.

Ответ. 1) если F > 1, каждое полено распиливается на два отрезка – длиной 0,2 и 0,8 метра; (15 баллов)

2) если 0 < F < 1, каждое полено распиливается на два отрезка по 0,5 метра. (15 баллов)

За два ответа 30 баллов

(3) Каждый из двух производителей имеет линейную функцию предельных издержек (при Q = 0 MC = 0). Функция спроса также линейна. Если первый производитель монополизирует весь рынок, то он выберет такой объем выпуска, при котором эластичность спроса по цене равна (-3). Аналогично второй производитель единолично монополизирует рынок при эластичности, равной (-2). Производителям не удалось договориться о каких-либо согласованных действиях на рынке, поэтому им пришлось вступить в конкуренцию. В результате на рынке установилась конкурентная цена, равная 24 при эластичности спроса (- ² / ₃). Какие цены (P ₁ и P ₂) установили бы производители, если бы они – либо тот, либо другой – оказались монополистами на данном рынке?

Решение

Известно, что e_р = - . Тогда при цене конкуренции Р_с = 24 выполняется:

- = - ; a = 60 b. При e_р = -3 выполняется: -3 = - ; 3 = ; P ₁ = 45. При e_р = -3 выполняется: -2 = - ; 2 = ; P ₂ = 40.

Ответ: P ₁ = 45, P ₂ = 40. (20 баллов)

(4) Один мальчик очень любит желтые и красные витаминки в драже. Первая желтая витаминка имеет для него предельную полезность, равную 28, каждая последующая - на 1 единицу меньше предыдущей. Первая красная витаминка имеет предельную полезность, равную 78, каждая последующая – на 3 единицы меньше предыдущей. Цена желтой витаминки 2 копейки, красной - 3 копейки. Сумма денег, которой располагает мальчик, равна 111 копейкам. Сколько желтых и сколько красных витаминок купит мальчик для того, чтобы максимизировать общую полезность?

Решение

Предположим, общая полезность максимизируется, если куплено Х желтых витаминок и Y красных.

Бюджетное ограничение: 111 = 2 Х + 3 Y. 3 Y = 111 – 2 X. Критерий оптимума потребителя:

= . = . 3 (29 – X) = 2 (81 – 3 Y).

3 (29 – X) = 2 (81 – 111 + 2 X). X = 21. Y = (111 – 2 X): 3 = 23.

Ответ: 21 желтая и 23 красных. (15 баллов)

(5) Один завод специализируется на производстве камнедробилок. Если он в течение года соберет одну камнедробилку, то затраты (ТС) составят 100 миллионов рублей. При увеличении годового выпуска на каждую последующую камнедробилку предельные затраты (МС) будут возрастать на 5 миллионов рублей. Рыночная цена камнедробилки равна 200 миллионам рублей. Сколько камнедробилок выпустит завод за год? [ ВНИМАНИЕ: в задаче по умолчанию предполагалось, что МС растут на 5 млн. рублей с увеличением выпуска на каждую единицу начиная с Q = 0 ].

Решение

Предельные затраты, связанные с выпуском N -й камнедробилки: MC = 5 N. Условие максимизации прибыли: MC = P. 5 N = 200. N = 40.

Ответ: 40. [Учитывая не совсем ясные условия задачи, комиссия засчитывала как правильный и ответ «41»]. (10 баллов)

(6) Функция полезности потребителя U = XY, P_x = 20 руб. Известно, что первая единица товара Y обходится потребителю в 1 рубль, вторая – в два рубля, третья – в три рубля и т.д. Хватит ли потребителю 60 рублей для того, чтобы обеспечить уровень полезности, равный 12 единицам?

Решение

Используя формулу суммы Y членов арифметической прогрессии, определим расходы потребителя на товар Y: .

Бюджет потребителя в целом: I = 60 = 20 X + . X = 3 - .

Определим значение U_max, которое может быть достигнуто при заданном бюджете.

U = [3 - ] Y = 3 Y - 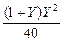. U_max достигается при условии: U ¢ = 0.

– 0,075 Y ²– 0,05 Y + 3 = 0. Решая уравнение, получаем: Y₁ = 6, Y₂ = - 6,667. Естественно, второй корень отбрасываем. X = 3 - = 1,95. При таких значениях Х и Y достигается значение функции полезности U_max = XY = 1,95 × 6 = 11,7 < 12.

Ответ. 60 рублей не хватит для достижения уровня полезности, равного 12. (25 баллов)

ИТОГО: 120 баллов

Максимальное количество баллов за тесты и задачи: 180

Дата добавления: 2015-09-06