|
Читайте также: |
1. Если декремент подстановки 
=(ia…bjc…d) ( (i) 
j и (j) i) равен 25, то декремент подстановки (ij) равен.
2. (ia…b), (jc…d) – независимые циклы. Если декремент подстановки =(ia…b) (jc…d) равен 13, то декремент подстановки (ij) равен.
3. i – неподвижный символ подстановки =(ja…b). Если декремент подстановки равен 18, то декремент подстановки (ij) равен.
4. Если декремент подстановки =(ija…b) (a i) равен 34, то декремент подстановки (ij) равен.
5. = 1 (ij) 2 - произведение попарно независимых циклов 1, (ij), 2. Если декремент подстановки равен 100, то декремент подстановки (ij) равен.
6. Если декремент подстановки =(ia…bjc…d) ( (i) j и (j) i) равен 20, то декремент подстановки (ij) равен.
7. (ia…b), (jc…d) – независимые циклы. Если декремент подстановки =(ia…b) (jc…d) равен 16, то декремент подстановки (ij) равен.
8. i – неподвижный символ подстановки =(ja…b). Если декремент подстановки равен 50, то декремент подстановки (ij) равен.
9. Если декремент подстановки =(ija…b) (a i) равен 44, то декремент подстановки (ij) равен.
10. = 1 (ij) 2 - произведение попарно независимых циклов 1, (ij), 2. Если декремент подстановки равен 15, то декремент подстановки (ij) равен.
11. Число подстановок x из S5, для которых (1 2 3 4 5) x = x (1 2), равно.
12. Число подстановок x из S4 таких, что x5 = e равно.
13. Число подстановок x из S4 таких, что x3 = e равно.
14. Число подстановок x из S3, удовлетворяющих равенству
((1 2 3) x)2 = (1 2 3)2 x2, равно.
15. Число подстановок x из S3, удовлетворяющих равенству
((1 2) x)-1 = (1 2)-1 x-1, равно.
16. Число подстановок x из S3, удовлетворяющих равенству
((1 3) x)3 = (1 3)3 x3, равно.
17. Число подстановок x из S3, удовлетворяющих равенству
((1 2 3) x)3 = (1 2 3)3 x3, равно.
18. Наименьшее число транспозиций при разложении подстановки (1 2 3)(4 5 6)
в произведение транспозиций равно.
19. Наименьшее число транспозиций при разложении подстановки (1 2 3)(1 3 6)
в произведение транспозиций равно.
20. Наименьшее число транспозиций при разложении подстановки (1 2 3)(1 3 6 7)
в произведение транспозиций равно.
21. Число подстановок, содержащихся во множестве
{ (1 2) x | x – четная подстановка из S4 } 
{(1 2 3)x | x 
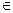S4},
равно.
22. Число подстановок, содержащихся во множестве
{ (1 2) x | x – четная подстановка из S5 } {(1 3)x | x – четная подстановка из S5}, равно.
23. Число подстановок, содержащихся во множестве
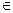{ (1 2) x | x – нечетная подстановка из S4 } {(1 2 3)x | x S4},
равно.
24. Число подстановок, содержащихся во множестве
{ (1 2) x | x – нечетная подстановка из S6 } {(1 2 3)x | x – нечетная подстановка из S6}, равно.
25. Число подстановок, содержащихся во множестве
{ (1 5) x | x – четная подстановка из S5 } {(1 2 3)x | x – четная подстановка из S5}, равно.
26. Число подстановок, содержащихся во множестве
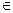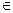{ (1 2 4) x | x S4 } {(1 2 3)x | x S4},
равно.
27. Число подстановок, содержащихся во множестве
{ (1 4) x | x 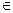S5 } {(1 3)x | x 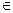S5}, равно.
28. Число подстановок, содержащихся во множестве
{ (1 2 4) x | x – четная подстановка из S5 }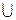 
{(2 3)x | x – нечетная подстановка из S5}, равно.
29. Число подстановок, содержащихся во множестве
{ (1 2 4) x | x – нечетная подстановка из S6 } 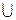{(2 3)x | x – четная подстановка из S6}, равно.
30. Число подстановок, содержащихся во множестве
{ (1 2) x | x – четная подстановка из S5 } 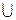{(2 3)x | x – нечетная подстановка из S5}, равно.
Дата добавления: 2015-09-06; просмотров: 168 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Понимание подошвы. | | | ПОРЯДОК |