Галактическая система координат. Старая и новая системы.

ГАЛО.

Границы нашей Галактики определяются размерами гало. Ра-диус гало значительно больше разме-ров диска и по некоторым данным достигает нескольких сот тысяч све-товых лет. Центр симметрии гало Млечного Пути совпадает с центром галактического диска.

Состоит гало в основном из очень старых, неярких мало массивных звёзд. Они встречаются как поодиночке, так и в виде шаровых скоплений, которые могут включать в себя более миллиона звёзд. Возраст населения сферической составляющей Галакти-ки превышает 12 млрд. лет. Его обыч-но принимают за возраст самой Га-лактики.

Характерной особенностью звёзд гало является чрезвычайно малая до-ля в них тяжёлых химических эле-ментов. Звёзды, образующие шаровые скопления, содержат металлов в сот-ни раз меньше, чем Солнце.

Звёзды сферической составляю-щей концентрируются к центру Га-лактики. Центральная, наиболее плот-ная часть гало в пределах нескольких тысяч световых лет от центра Галак-тики называется балдж (в переводе с английского “утолщение”).

Звёзды и звёздные скопления гало движутся вокруг центра Галактики по очень вытянутым орбитам. Из-за того, что вращение отдельных звёзд происходит почти беспорядочно (т. е. скорости соседних звёзд могут иметь самые различные направления), гало в целом вращается очень медленно.

ДИСК.

По сравнению с гало диск вращается заметно быстрее. Скорость его вращения не одинакова на раз-личных расстояниях от центра. Она быстро возрастает от нуля в центре до 200--240 км/с на расстоянии 2 тыс. световых лет от него, затем не-сколько уменьшается, снова возраста-ет примерно до того же значения и далее остаётся почти постоянной. Изучение особенностей вращения диска позволило оценить его массу. Оказалось, что она в 150 млрд. раз больше массы Солнца.

Население диска очень сильно от-личается от населения гало. Вблизи плоскости диска концентрируются молодые звёзды и звёздные скопле-ния, возраст которых не превышает нескольких миллиардов лет. Они об-разуют так называемую плоскую со-ставляющую. Среди них очень много ярких и горячих звёзд.

Газ в диске Галактики также сосре-доточен в основном вблизи его пло-скости. Он распределён неравномер-но, образуя многочисленные газовые облака -- от гигантских неоднород-ных по структуре сверх облаков про-тяжённостью несколько тысяч свето-вых лет до маленьких облачков размерами не больше парсека.

Основным химическим элемен-том в нашей Галактике является водо-род. Приблизительно на 1/4 она со-стоит из гелия. По сравнению с этими двумя элементами остальные при-сутствуют в очень небольших количе-ствах. В среднем химический состав звёзд и газа в диске почти такой же, как у Солнца.

Галактическая система координат. Старая и новая системы.

Главной системой координат, используемой в звёздной астрономии, является галактическая система координат. Экваториальная система координат, которую обычно астрономы используют для определения положений и движений небесных объектов, никак не связана с положениями и движением этих объектов в Галактике. То же можно сказать и об эклиптической системе координат. Галактическая система координат непосредственно связана с существованием в нашей Галактике сильной концентрации многих объектов к плоскости Млечного Пути. Для этой системы координат основной плоскостью является плоскость симметрии нашей Галактики. Отметим, что Солнце не лежит в плоскости Галактики, его положение смещено приблизительно на 10 парсек в сторону северного галактического полюса. Северный полюс Галактики находится в созвездии Волосы Вероники и для него в настоящее время приняты следующие значения экваториальных координат AG = 192њ.85948, DG = +27њ.12825 на равноденствие 2000.0 (до недавнего времени принимали AG = 12h49m = 192њ.25, DG = +27њ.4 на равноденствие 1950.0). Южный полюс Галактики находится в созвездии Скульптора. Галактическая долгота l отсчитывается от направления на центр Галактики против часовой стрелки, если смотреть с ее северного полюса. Галактическая широта b отсчитывается от плоскости Галактики в направлении ее полюса, прочем широта cчитается положительной по направлению к северному полюсу Галактики, и отрицательной - к южному. Галактические координаты не меняются со временем, как меняются экваториальные координаты вследствие прецессии земной оси, так как с Землей они не связаны.

Рассмотрим переход от экваториальных координат к галактическим. Ранее для этого широко использовались таблицы, которые приводились в любом руководстве по звёздной астрономии. В настоящее время используют соответствующие программы. На рис.1-1 показана небесная сфера, на которой указаны северный полюс мира (Pm), северный полюс Галактики (Pg) и объект S. Для полярного треугольника легко записать формулы, связывающие экваториальные и галактические координаты:

Указанная на рис.1-1 и в формулах (1-1) величина la отсчитывается от точки пересечения небесного и галактического экваторов (величина галактической долготы восходящего узла галактического экватора в настоящее время принята равной 32њ.93192), а не от направления на центр Галактики. Поэтому, чтобы получить значения галактических долгот, отсчитываемых от центра Галактики, необходимо добавить к величинам, получаемым из выражений (1-1), поправку, равную галактической долготе северного полюса мира - 122њ.93192.. (Отметим, что поскольку галактическая долгота изменяется в диапазоне (0њ - 360њ), для ее правильного определения необходимы два уравнения.)

До 1970г. иногда использовалась старая (так называемая - первая) система галактических координат, где долгота как раз и отсчитывалась от точки пересечения небесного и галактического экваторов. В старой галактической системе, обозначавшейся верхним индексом I, координаты центра Галактики были равны l1=327њ.69 и b1=-1њ.40 В старых работах и в некоторых каталогах новые галактические координаты (вторая система) обозначались индексом II. Вторая система галактических координат изначально была основана на радионаблюдениях нейтрального водорода, но после запуска искусственного спутника Hipparcos были уточнены координаты Северного полюса Галактики. В настоящее время последние уточнения утверждены съездом МАС.

Формулы для пересчёта собственных движений из экваториальной системы координат в галактическую легко получить дифференцированием выражений (1-1) по времени, считая экваториальные координаты функциями времени, так как собственные движения представляют собой изменения со временем угловых координат объектов. Можно поступить и по другому. Чтобы получить вектор с компонентами (µ l, µb) из вектора (µl, µb), необходимо осуществить поворот системы координат, связанной с объектом S на угол, составляемый на небесной сфере большими кругами, проходящими через объект и полюс мира, объект и полюс Галактики (см. рис.1-1). В этом случае:

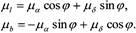
Выражения для тригонометрических функций угла φ легко получить, рассматривая полярный треугольник на рис. 1-1 (приводятся окончательные выражения):

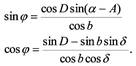
4. Пространственные скорости звезд

Скорость, с которой звезда движется в пространстве относительно Солнца, назовем пространственной скоростью. Обозначим вектор пространственной скорости одной из звезд через v. Его можно представить как сумму двух составляющих векторов, один из которых (тангенциальная скорость v_t) перпендикулярен лучу зрения (т. е. направлению звезда – наблюдатель), а другой направлен по лучу зрения (лучевая скорость v_r). Тогда по теореме Пифагора модуль пространственной скорости будет равен:

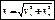
2. Эффект Доплера и определение лучевых скоростей. Лучевые скорости определяют по спектрам звезд. При этом используется явление, которое называется эффектом Доплера. Сущность эффекта Доплера состоит в том, что линии в спектре источника, приближающегося к наблюдателю, смещены к фиолетовому концу спектра, а линии в спектре удаляющегося источника – к красному концу спектра (по отношению к положению линий в спектре неподвижного источника).

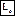– длина волны, которую принимает наблюдатель от неподвижного источника;

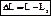
с – скорость света.

5. Собственные движения звезд и методы их определения

Собственным движением называются изменения координат звёзд на небесной сфере, вызванные относительным движением звёзд и Солнечной системы. В них не включают периодические изменения, вызванные движением Земли вокруг Солнца (параллакс).

Более строгое определение: «Собственным движением звезды в астрономии называют величины, характеризующие её угловое перемещение на небесной сфере в заданной системе координат за единицу времени»

Если какая-либо звезда наблюдалась дважды в эпоху и эпоху и её видимые координаты — прямое восхождение (α) и склонение (δ) — приведены в систему фундаментального каталога FK5(эпоха T0), то её собственное движение определяется как

размерность — секунда времени в год,

размерность — угловая секунда в год.

Определённые таким способом собственные движения звёзд иногда называют меридианными, так как они определяются в результате сравнения двух положений, полученных посредством наблюдений на меридианных кругах. Массовые определения меридианных собственных движений звёзд стали возможными уже в XIX веке в результате создания нескольких десятков меридианных каталогов, приведённых к некоторой одной фундаментальной системе. Наибольшее число (33 342) положений и собственных движений звёзд (в том числе слабых — до 9-й звёздной величины) в одной системе приведено в известном общем каталоге «General Catalogue» Льюиса Босса (1910 год). Ошибки собственных движений в этом каталоге составляют ± (0.005—0.15)″/год. Положения и движения звёзд несвободны от систематических ошибок. Новые фундаментальные каталоги звёзд FK4 и FK5 сохраняют ошибки собственных движений на уровне ± (0.002—0.005)″/год, однако эти каталоги охватывают лишь небольшое число избранных, в основном ярких звёзд. К 1995 году было известно не менее 50 000 меридианных собственных движений звёзд от самых ярких до 9-й звёздной величины. Ошибки этих собственных движений могут быть от ± 0.002″ до ± 0.010″ в зависимости от продолжительности истории наблюдений. По величине большинство известных собственных движений меньше 0.050″/год, однако встречаются и большие собственные движения. Так, самое высокое значение собственного движения имеет «летящая» Звезда Барнарда — 10.358″. Вторую и третью строчку в рейтинге самых быстро перемещающихся звёзд на небесной сфере занимают Звезда Каптейна (8.670″/год) и Лакайль 9352 (6.896″/год).

Связь между расстоянием и собственным движением звезды определяется из соотношения:

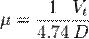
Здесь 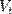— проекция на небесную сферу пространственной скорости звезды в системе координат, движущейся вместе с Солнцем, D — расстояние до звезды в парсеках (1 пк = 206 265 астрономических единиц = 3,26 световых лет). Размерность — км/с, размерность ″ — угловая секунда в год.

В конце XIX века в практику наблюдательной астрономии прочно внедрилась фотография. В связи с этим развились фотографические методы определения собственных движений звёзд.

Фотографические собственные движения звёзд определяются сравнением измеренных положений звёзд на различных пластинках, полученных в разные эпохи. В силу этого фотографические собственные движения неизбежно остаются относительными, то есть определяют движение одних звёзд относительно некоторой группы других звёзд (так называемых опорных звёзд), о движении которых делаются более или менее правдоподобные предположения. Таким образом, чтобы перейти от фотографических собственных движений звёзд к меридианным (имеющим смысл инерциальных или «абсолютных»), необходимо выполнить дополнительное исследование, которое астрономы иногда называют абсолютизацией и которое редко бывает безупречным.

Главное достоинство фотографических собственных движений в их относительно высокой точности и массовости в отношении самых слабых звёзд. Это обстоятельство делает их незаменимым наблюдательным материалом при статистических исследованиях, связанных с определением дисперсий пекулярных (индивидуальных) движений звёзд и распределением движений звёзд, отнесенных к разным типам звёздного населения.

Существенным недостатком фотографических собственных движений звёзд является их несвобода от разного рода систематических ошибок, связанных с фотографическим методом наблюдений. Это так называемые ошибки «уравнения блеска», «уравнения цвета» и некоторые другие, связанные с несовершенством оптики широкоугольных телескопов, применяемых в астрофотографии. Перечисленные ошибки выражаются в систематическом смещении изображений звёзд на пластинке в зависимости от яркости, цвета звёзд и их положения на пластинке. Эти ошибки трудно калибруются, так как они зависят ещё от постоянно изменяющихся условий наблюдений (прозрачности атмосферы, ветра, качества изображений).

6. Методы определения лучевых скоростей звезд.

Лучевая скорость - скорость изменения расстояния между объектом и наблюдателем. Метод определения лучевой скорости звёзд, галактик и др. астрономич. объектов основан на использовании эффекта Доплера. Л. с. определяется по смещению линий (излучения или поглощения) в спектре источника или по изменению частоты отражённого сигнала при радиолокации.

Если относительное изменение длины волны 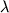вследствие эффекта Доплера 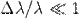, то Л. с. связана с ним соотношением: 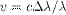. В случае 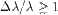связь этой величины со скоростью становится более сложной. В близких к Солнцу окрестностях Галактики звёзды имеют Л. с. примерно от -100 до +240 км/с, скорости наиболее удалённых квазаров приближаются к скорости света. Л. с. звёзд и галактич. облаков газа, вращающихся вокруг центра Галактики, зависит от движения Солнца в Галактике и хаотич. скоростей этих объектов. Зная параметры, характеризующие вращение Галактики, а также Л. с. и координаты звёзд и облаков межзвёздного газа, движущихся по орбитам, близким к круговым, можно определить, на каких расстояниях они от нас находятся. Л. с. галактик также может служить критерием расстояния до них.

Л. с. отдельных излучающих атомов может быть различной, что влияет на профиль спектральных линий, расширяет их. Поэтому анализ профилей линий даёт ценную информацию о движении вещества источника (тепловом, турбулентном или упорядоченном). Напр., широкие профили всех спектр. линий излучения наблюдаются у быстровращающихся звёзд и у звёзд, с поверхности к-рых происходит истечение газа. Определение Л. с. отдельных компонентов кратных звёздных систем (напр.,двойных звёзд) или систем галактик позволяет оценить массы этих систем. Знание распределения Л. с. звёзд и газа по диску галактик даёт возможность оценить их массу и плотность

Лучевые скорости звезд. Динамическая картина Вселенной может быть установлена, если известны скорости движения звезд относительно наблюдателя. Эти вопросы связаны со значительными трудностями. Ниже рассматриваются способы определения скоростей небесных светил.

Если некоторое светило движется относительно наблюдателя А, то скорость v его движения может быть разложена на две составляющие. Составляющая, представляющая проекцию скорости на луч зрения или радиус-вектор, называется лучевой скоростью звезды, а трансверсальная составляющая скорости, перпендикулярная лучу зрения, называется собственным движением.
Каждая из этих составляющих определяется особым методом. Метод определения лучевых скоростей основан на использовании принципа Допплера - Физо - Белопольского. Согласно, этому принципу, скорость светила по лучу зрения определяется по смещению спектральных линий в спектре:
где X - длина волны спектральной линии, ДЯ - изменение длины волны в результате движения источника света по лучу зрения, лучевая скорость и с - скорость света.

Трудности в измерении лучевых скоростей звезд возникают из-за того, что эти скорости обычно малы по сравнению со скоростью света, и вследствие этого смещение спектральных линий очень незначительно. Только сравнивая фотографии спектров, удается обнаружить и измерить это смещение. Заметим, что лучевые скорости звезд сравнимы со скоростью Земли в ее движении вокруг Солнца, которая равна примерно 30 км /сек.

7. Звездные тригонометрические параллаксы.

ТРИГОНОМЕТРИЧЕСКИЙ ПАРАЛЛАКС, метод измерения расстояния до звезды, использующий принцип ТРИАНГУЛЯЦИИ. При обращении Земли вокруг Солнца положение ближайших звезд на небосводе слегка изменяется по отношению к более удаленным звездам. Эти изменения можно измерить по фотографиям, сделанным с промежутком в полгода, т. е. когда Земля находится в диаметрально противоположных точках орбиты. Угловое смещение дает непосредственное измерение ПАРАЛЛАКСА звезды. Посколькуоснование треугольника известно (по расстоянию от Земли до Солнца), расстояние до звезды можно вычислить методами ТРИГОНОМЕТРИИ. Впервые этот метод был применен в 1838 г. Фридрихом БЕССЕЛЕМ при измерении расстояния до звезды 61 Лебедя. Параллакс измеряется в дуговых секундах. Величина, обратная параллаксу, есть расстояние до звезды в ПАРСЕКАХ. Альфа Центавра - звезда с самым большим известным параллаксом, 0,752", соответствующим расстоянию в 1,3 парсека. Стандартная ошибка при измерении параллакса по фотографиям составляет около 0,01", но если использовать добавочные фотопластинки, ошибку можно снизить до 0,004". Параллаксзвезды, находящейся на расстоянии 25 парсеков, равен 0,04", так что погрешность составляет около 10%. Спутник «Гиппарх» может измерять параллакс более точно.

Метод определения тригонометрических параллаксов даже для ближайших звездных скоплений дает пока не очень надежные результаты, так как все скопления расположены дальше 20 парсек от Солнца, а параллаксы меньшие, чем 0",05, обременены трудно учитываемыми систематическими ошибками, связанными в основном с проблемой абсолютизации относительных тригонометрических параллаксов. Среди небольшого числа опорных звезд, относительно которых определяется параллакс данной звезды, могут оказаться звезды более близкие к Солнцу, чем эта звезда. Однако на тригонометрических параллаксах в значительной степени основана калибровка многих других методов определения расстояний до звезд и звездных скоплений, поэтому для членов ближайших к Солнцу скоплений эти параллаксы неоднократно определялись и продолжают определяться. С течением времени точность их постепенно возрастает в связи с переходом к использованию большего числа более слабых опорных звезд и совершенствованием методики обработки результатов измерений, описанным, например, в статье Василевскиса (1966).

Уже сейчас получаются (Апгрен, 1974), по-видимому, совершенно реальные значения тригонометрических параллаксов слабых членов Гиад, находящихся на расстоянии 46 пс от Солнца.

Сравнительно недавно Томас (1969) предложил даже обширную программу определения с точностью до ±0",0005 (!) тригонометрических параллаксов членов скопления Ясли, находящегося на расстоянии 175 пс от Солнца. Так как ошибка dMопределения абсолютной величины M звезды связана с ошибкой dπ определения ее параллакса π (при отсутствии корреляции между π и dπ) соотношением

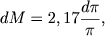
то осуществление подобной программы позволило бы определить абсолютные величины звезд этого скопления с точностью до ±0m,2. Насколько реально выполнение этой программы, покажет будущее.

8. Абсолютная звездная величина

Абсолютная звёздная величина (M) для звёзд определяется как видимая звёздная величина объекта, если бы он был расположен на расстоянии 10 парсек от наблюдателя. Абсолютная болометрическая (то есть учитывая все спектры электромагнитных волн) звёздная величина Солнца +4,7.

Если известна видимая звёздная величина 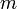и расстояние до объекта 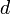, можно вычислить абсолютную звёздную величину по формуле:

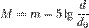
где 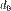= 10 пк ≈ 32,616 световых лет

Соответственно, если известны видимая и абсолютная звёздные величины, можно вычислить расстояние по формуле

Абсолютная звёздная величина связана со светимостью следующим соотношением:

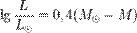
где 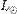и — светимость и абсолютная звёздная величина Солнца

Для объектов Солнечной системы (планет, астероидов и комет) используется другая версия абсолютной звёздной величины^[1]. Для них абсолютная величина принимается равной видимой величине, которую они имели бы на расстоянии 1 а. е. от Солнца и от наблюдателя, причём наблюдатель должен видеть полную фазу объекта (то есть теоретически наблюдатель должен находиться в центре Солнца).

Следует заметить, что для самосветящихся объектов

H = M − 31,57.

Есть набор расчетных таблиц для тел с наиболее распространнёнными значениями альбедо астероидов (0,25 — 0,05)

Дата добавления: 2015-10-13