Покрытия и раскраски

Некоторые задачи, возникающие при планировании производства, составлении графиков осмотра и транспортировки товаров, могут быть представлены как задачи теории графов, тесно связанные с так называемой «задачей раскраски». Эта задача формулируется следующим образом: для данного графа определить минимальное количество цветов, необходимых для раскраски вершин графа так, чтобы никакие две смежные вершины не были окрашены в один цвет.

Задачи раскраски вершин или ребер графа занимают важное место в теории графов. К построению раскрасок сводится целый ряд практических задач. Характерной особенностью этих задач является существование объек­тов, которые по каким-либо причинам не могут быть объ­единены в одну группу.

Пусть G – некоторый граф, k – натуральное число. Произвольная функция вида f: X ®{l,2,..., k }назы­вается вершинной k-раскраской, или просто k-раскраской, графа G. Если позволяет контекст, то k в этом определе­нии опускается. Раскраска называется правильной, если f(x_i) ¹ f(x_j) для любых смежных вершин x_i и x_j. Граф, для которого существует правильная k -раскраска, называется k-раскрашиваемым (или раскрашиваемым k цветами). В определении раскраски вместо множества {1, 2,..., k }можно взять произвольное k -элементное множество.

Правильную k -раскраску графа можно трактовать как окрашивание каждой его вершины в один из k цветов, при этом смежные вершины должны получать различ­ные цвета. Поскольку функция f не обязательно сюрьективна, то при k -раскраске фактически может быть ис­пользовано менее k цветов. Таким образом, правильную k -раскраску графа G можно рассматривать как разбие­ние

X ₁È X₂ È... È X_l = X, l£k,

множества вершин X на не более чем k непустых клас­сов, каждый из которых является независимым множест­вом. Классы этого разбиения называются цветными классами. Множество вершин одного цвета называетсяодноцветным клаcсом.

Минимальное число k, при котором граф G является k -раскрашиваемым, называется хроматическим числом этого графа и обозначается (G). Если (G) = k, то граф G называется k-хроматическим. Правильная k -раскраска графа G при k= (G) называется минимальной.

В качестве иллюстрации рассмотрим граф G, изобра­женный на рис. 4.28, где указана одна из правильных 4-раскрасок. Меньшим числом цветов этот граф раскра­сить правильно нельзя. Действительно, граф содержит цикл (x₁, x₂, x₃, x₄, x₅, x₁), для правильной раскраски которого нужно не менее трех цветов, а для вершины x₆ требуется новый цвет. Итак, g(G)=4.

Пример. Так как в полном графе К_п любые две различные вершины связаны ребром, то g (К_n)= п.

Рассмотрим некоторые практи­ческие задачи, сводящиеся к пра­вильной раскраске графов.

1. Задача составления расписа­ний. Предположим, что нужно про­честь несколько лекций за крат­чайшее время. Чтение каждой лек­ции в отдельности занимает один час, но некоторые лекции не мо­гут читаться одновременно (например, их читает один и тот же лектор). Построим граф G, вершины которого би­ективно соответствуют лекциям, и две вершины смежны тогда и только тогда, когда соответствующие лекции нель­зя читать одновременно. Очевидно, что любая правильная раскраска этого графа определяет допустимое расписание: лекции, соответствующие вершинам графа, составляющим цветной класс, читаются одновременно. И, обратно, любое допустимое расписание определяет правильную раскраску графа G. Оптимальные расписания соответствуют мини­мальным раскраскам, а число часов, необходимое для про­чтения всех лекций, равно g (G).

2. Задача распределения оборудования. Заданы мно­жества Х = { х₁, х₂,..., х_n }и S = { s_1, s₂,..., s_m }работ и механизмов соответственно. Для выполнения каждой из работ требуется некоторое время, одинаковое для всех работ, и некоторые механизмы. При этом никакой из ме­ханизмов не может быть одновременно занят в несколь­ких работах. Нужно распределить механизмы так, чтобы общее время выполнения всех работ было минимальным. Построим граф G с множеством вершин X и объявим верши­ны х_i и х_j (i≠j) смежными тогда и только тогда, когда для выполнения работ х_i и х_j требуется хотя бы один общий механизм. При правильной раскраске графа G ра­боты, соответствующие вершинам одного цвета, можно выполнять одновременно, а наименьшее время выполне­ния всех работ достигается при минимальной раскраске.

3. Задача о проектировании коробки скоростей. Короб­ка скоростей – механизм для изменения частоты враще­ния ведомого вала при постоянной частоте вращения ве­дущего. Это изменение происходит за счет того, что на­ходящиеся внутри коробки шестерни (зубчатые колеса) вводятся в зацепление специальным образом. Одна из задач, стоящая перед конструктором коробки, заключает­ся в минимизации ее размеров, а это часто сводится к минимизации числа валов, на которых размещаются шестерни.

Построим граф G, вершины которого биективно соот­ветствуют шестерням. Если по какой-то причине две шестерни не должны находиться на одном валу (напри­мер, они могут быть в зацеплении, или их общий вес велик для одного вала и т. д.), то соответствующие вер­шины графа соединим ребром. Вершины, имеющие один цвет при правильной раскраске этого графа, определяют шестерни, которые могут находиться на одном валу, а хроматическое число g (G) равно минимальному коли­честву валов, нужных для проектируемой коробки.

4. Рассмотрим граф G, вершины которого – страны, а ребра соединяют страны, имеющие общую границу. Числу g (G) соответствует наименьшее число красок, необходимых для раскраски карты так, чтобы никакие две соседние страны не были окрашены в один цвет.

Для некоторых графов хроматические числа найти не­сложно. Например, g (К_п) = п, g(K_n,m) = 2, g(C_2n) = 2, g(C _{2 n +1}) = 3.

Очевидно, что граф является 1-хроматическим тогда и только тогда, когда он пустой, а 2-хроматическим – когда он двудольный и непустой. Обычно 2-хроматический граф называют бихроматическим.Поэтому теорему Кёнига о двудольных графах можно сформулировать в следующем виде.

Теорема 4.10.1. Непустой граф является бихроматическим тогда и только тогда, когда он не содержит цик­лов нечетной длины.

Задачи определения хроматического числа и построе­ния минимальной раскраски произвольного графа явля­ются очень сложными, эффективные алгоритмы их ре­шения неизвестны. Рассмотрим простой эвристический алгоритм построе­ния правильной раскраски вершин графа, в ряде случаев приводящий к раскраскам, близким к минимальным.

Замечание. Данный алгоритм определяет оценку y '(G) хроматического числа g(G) графа G, которая удовлетворяет соотношению

g(G) £y'(G) £ max min { d (i)+l, i },

i

где d (i) – степень i -ой вершины, причем индексация вершин х_i осуществляется в соответствии с убыванием их степеней.

Шаг 1. G – данный граф. Для каждой вершины графа определить ее степень. Расположить вершины в порядке невозрастания их степеней.

Шаг 2. Первая вершина окрашивается в цвет №1. Затем список вершин просматривается сверху вниз и в цвет №1 окрашивается всякая вершина, которая не смежна с другой, уже окрашенной в этот цвет.

Шаг 3. Возвращаемся к первой в списке неокрашенной вершине, окрашиваем ее в цвет №2 и, двигаясь по списку, окрашиваем вершины в цвет №2 так же, как окрашивали в цвет №1.

Шаг 4. Процедура продолжается до тех пор, пока все вершины не будут окрашены. Количество использованных цветов будет приближенным значением хроматического числа.

Раскраска, к которой приводит описанный алгоритм, называется последовательной. Очевидно, что это – пра­вильная раскраска. Для некоторых классов графов (на­пример, полных k -дольных) последовательная раскраска является минимальной. В общем случае это не так.

Следующая теорема сводит задачу построения пра­вильной раскраски графов к аналогичной задаче для двухсвязных графов.

Теорема 4.10.2. Если каждый блок графа k -раскраши-ваем, то и сам граф также k -раскрашиваем.

Доказательство. Воспользуемся индукцией по числу блоков рассмат­риваемого графа. Для графа, являющегося блоком, ут­верждение тривиально. Предположим, что теорема верна для графов, состоящих из m /1 блоков. Пусть теперь G – граф, имеющий ровно m+ 1 блоков, В – один из его концевых блоков, Н – объединение всех остальных бло­ков. По индуктивному предположению оба графа В и H являются k -раскрашиваемыми. Зафиксируем для каждого из них правильную k -раскраску.

Графы В и H имеют ровно одну общую вершину х. Если ее цвета в обеих фиксированных k -раскрасках сов­падают, то получена правильная k -раскраска графа G. В противном случае нужно очевидным образом переста­вить цвета в одной из фиксированных раскрасок. Теорема доказана.

Утверждение 4.10.1. Если граф G является r -хромати-ческим, то он может быть раскрашен с использованием r красок с помощью следующей процедуры: сначала в один цвет окрашивается некоторое максимальное независимое множество S [ G ], затем окрашивается в следующий цвет множество S [ X \ S [ G ]] и т.д. до тех пор пока не будут раскрашены все вершины.

Утверждение 4.10.2. Каждый планарный граф 5-раскра-шиваем.

Утверждение 4.10.3. Каждый планарный граф, не содержащий треугольников, 3-раскрашиваем.

Утверждение 4.10.4. Хроматическое число графа G равно кликовому числу его дополнения ` .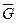

Реберной раскраской неорграфа G =(X, V) k цветами называется функция

j: V ®{l,2,.., k },

такая, что для любых двух смежных ребер v₁ и v₂ выполняется j (v ₁)¹ j (v ₂).

Хроматическим индексом графа G называется наименьшее такое k, что граф G допускает реберную раскраску k цветами.

Существуют и практические задачи, связанные с раскраской ребер в мультиграфе.

Раскраска ребер в мультиграфе G может быть определена с помощью раскраски вершин так называемого реберного мультиграфа L(G). Для произвольного неориентированного мультиграфа G={X, V, Р}, где X – множество вершин, V – множество дуг, Р Î V X V, (x,v,y) Î Р тогда и только тогда, когда дуга v исходит из вершины х и заходит в вершину у, реберным мулътиграфом L(G) называется тройка { V, X, Р’}, где Р'ÎV X V, и выполняется (u, х, v)ÎР' тогда и только тогда, когда в мультиграфе G вершина х является концом ребер и и v. Раскраской ребермультиграфа G называется раскраска вершин мультиграфа L(G).

Пример. Проводится монтаж аппаратуры. Чтобы не перепутать проводники, необходимо их окрасить таким образом, чтобы два проводника, идущие к одной плате, имели разные цвета. В этом случае вершинами являются платы, а ребрами – проводники.

Теорема 4.10.3. Пусть G –неорграф без петель, имеющий хотя бы одно ребро. Тогда следующие условия эквивалентны:

1) G – бихроматический граф;

2) G – двудольный граф;

3) G не содержит циклов нечетной длины.

Теорема 4.10.4.Для любого неорграфа G без петель выпол­няется неравенствоg (G) £ d(G) +1, где d(G) – наибольшая степень вершин графа.

Дата добавления: 2015-10-13