Достижимость

Вершина графа х_i называется достижимой из вершины x_j того же графа, если существует по крайней мере один путь из x_i в x_j.

Множество вершин R(x_i), достижимых из некоторой вершины , определяется следующим выражением:

(2.9)

Действительно, первым элементом множества R(x_i) является вершина x_i, которая достижима из себя самой с помощью пути длины нуль; Г(x_i) – множество вершин x_j, достижимых из x_i с использованием путей длины единица; Г²(x_i) – множество вершин, достижимых из x_i с использованием путей длины два; - множество вершин, достижимых из x_i с использованием путей длины p. Таким образом, множество R(x_i) получается путем последовательного выполнения слева направо операции объединения в выражении (2.9) до тех пор, пока мощность текущего множества не перестанет увеличиваться при очередной операции объединения. С этого момента последующие операции объединения не будут давать новых элементов множеству R(x_i). Число объединений, которые необходимо выполнить, зависит от графа G. Но если граф конечен, то p<n, где n – число вершин графа.

Матрицей достижимостей называется квадратная матрица порядка n, элемент которой d_i,j =1, если , и d_i,j=0 в противном случае.

Пример. Построить матрицу достижимостей графа G, представленного на рис. 2.6.

Рис. 2.6

Решение. X={x₁, x₂, x₃, x₄}; Г(х₁)={x₂}; Г(х₂)={x₃}; Г(х₃)={x₄}; Г(х₄)={x₃}.

;

;

;

.

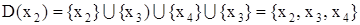Следовательно, матрица достижимостей имеет вид:

.

Очевидно, что элементы d_i,i=1, i=1, 2, …, n, так как каждая вершина достижима из себя самой.

Матрица контрдостижимостей (обратных достижимостей) определяется следующим образом:

где Q(x_i) – множество таких вершин x_iÎX, что из любой вершины этого множества можно достигнуть вершину x_i:

(2.10)

где - множество вершин, из которых достижима вершина x_i с исполь-зованием пути длины единица; ) – множество вершин, из которых достижима вершина x_i с использованием пути длины два и т.д. Операция объединения в выражении (2.10) выполняется слева направо до тех пор, пока очередное объединение не перестанет изменять “текущее множество”.

Пример. Построить матрицу контрдостижимостей Q для графа G рис. 2.6.

Решение.

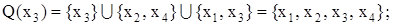
Матрица контрдостижимостей будет иметь вид:

.

Из определения матриц D и Q следует, что Q=D^T. Так как D(x_i) является множеством вершин, достижимых из 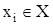, а Q(x_j) – множество вершин, из которых достижима вершина x_j, то D(x_i) 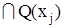- множество таких вершин, каждая из которых принадлежит по крайней мере одному пути, идущему от x_i к x_j. Эти вершины называются существенными (неотъемлемыми) относительно двух концевых вершин x_i и x_j. Вершины называются несущественными (избыточными), так как их удаление не влияет на пути от x_i к x_j.

Дата добавления: 2015-10-13