Для сложных процентов

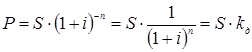
где k_д – дисконтный множитель для сложных процентов.

Если начисление процентов производится m раз в год, то формула примет вид:

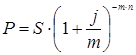
Пример. Через два года фирме потребуются деньги в размере 30 млн руб., какую сумму необходимо сегодня поместить в банк, начисляющий 25% годовых, чтобы через 2 года получить требуемую сумму?

Решение:

Поскольку срок финансовой операции составляет более года, то используем формулу приведения для сложных процентов:

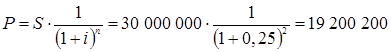руб.

или P = S • k_д = 30'000'000 • 0,6400000 = 19'200'000 руб.

Таким образом, фирме следует разместить на счете 19'200'000 руб. под 25% годовых, чтобы через два года получить желаемые 30'000'000 руб.

Современная величина и процентная ставка, по которой проводится дисконтирование, находятся в обратной зависимости: чем выше процентная ставка, тем при прочих равных условиях меньше современная величина.

В той же обратной зависимости находятся современная величина и срок финансовой операции: чем выше срок финансовой операции, тем меньше при прочих равных условиях современная величина.

Дата добавления: 2015-09-03