Множество Мандельброта – пример алгебраического фрактала

Множество Мандельброта — это фрактал определённый как множество точек на комплексной плоскости, для которых итеративная последовательность не уходит в бесконечность; Zi и C - комплексные переменные.

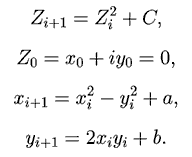
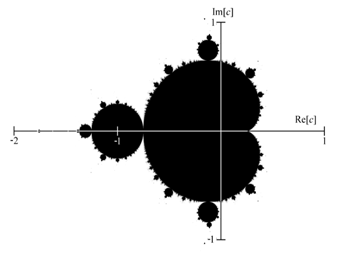
Берется точка комплексной плоскости с координатами (a,b), соответствующая комплексному числу c=a+bi. К этой точке n раз применяется преобразование. Если в результате n преобразований точка удалится на 2 или более единицы от начала координат, то она не принадлежит множеству Мандельброта, она окрашивается в белый цвет.
Если же расстояние от этой точки до начала координат при любом числе итераций n (допустим n=200) останется меньше 2, то точка принадлежит множеству Мандельброта и она окрашивается в черный цвет.

Для получения цветного изображения фрактала, точки, принадлежащие множеству Мандельброта, окрашиваются в цвет, зависящий от числа итераций

Первые исследования в этом направлении начались в начале XX века и связаны с именами французских математиков Гастона Жулиа и Пьера Фату. В 1918 году вышел почти двухсотстраничный труд Жулиа, посвященный итерациям комплексных рациональных функций, в котором описаны множества Жулиа – целое семейство фракталов, близко связанных с множеством Мандельброта. Этот труд был удостоен приза Французской академии, однако в нем не содержалось ни одной иллюстрации, так что оценить красоту открытых объектов было невозможно. Несмотря на то что это работа прославила Жулиа среди математиков того времени, о ней довольно быстро забыли.

Вновь внимание к ней обратилось лишь полвека спустя с появлением компьютеров, именно они сделали видимыми богатство и красоту мира фракталов

В 1982 году вышла книга Мандельброта «Фрактальная геометрия природы», в которой автор собрал и систематизировал практически всю имевшуюся на тот момент информацию о фракталах и в легкой и доступной манере изложил ее. Благодаря иллюстрациям, полученным при помощи компьютера фракталы стали известны широкой публике. Их успех среди не математиков во многом обусловлен тем, что с помощью весьма простых конструкций и формул, которые способен понять и старшеклассник, получаются удивительные по сложности и красоте изображения. Когда персональные компьютеры стали достаточно мощными, появилось даже целое направление в искусстве – фрактальная живопись, причем заниматься ею мог практически любой владелец компьютера.

Слайд 6

Фрактальная монотипия— вид фрактальных рисунков, которые получены методом монотипии. Фрактальная монотипия - естественный фрактал на акриле. Впервые применил технику монотипии в XVII столетии итальянский художник Джованни Кастильоне. Монотипию изготавливают так: на твердую поверхность наносят краски, сверху помещают лист бумаги и прижимают его к поверхности... На бумаге образуется оттиск с необычными узорами, которые не могут быть повторены художником.

Слайд 7

Фрактальная природа монотипии была обнаружена в 2000 г. химиком В. М. Лившицем и математиком В. В. Скворцовым, независимо друг от друга.

Ими же был предложен и термин «фрактальная монотипия».

В 1981 г. в г.Кохтла-Ярве (Эстония) состоялась первая выставка фрактальных монотипий художницы Леа -Тути Лившиц (1930—1999). Этот вид монотипии художница называла стохатипией. Сто́хатипия — вид монотипии, который состоит из стохастических фракталов, полученных естественным способом. Наиболее ценными считаются фигуральные стохатипии, так как вероятность возникновения образа человека при изготовлении стохатипии значительно меньше, чем пейзажа. Стохатипии, как фрактальные рисунки, бывают двух типов: оригинальные монотипии и адаптированные (дорисованные) художником к его замыслу. Стохастические рисунки являются видом модернизма в изобразительном искусстве.

Таким образом, фрактальную монотипию можно отнести к фрактальному искусству, причем получаемому не на компьютерах, а физико-химическим способом.

Слайд 8

Фрактальная живопись Эшера.
Мориц Корнелис Эшер, единственный в своем роде художник, работавший не столько с образами, сколько с понятиями.
Возможно, вы никогда не слышали этого имени. Но в любом случае, вы обязательно видели его картины. Гравюры, с изображением замкнутой лестницы, идущей все время вверх, дома с невероятно переплетенными колоннами, мозаики, или как их называют - паркеты из повторяющихся фигур людей, животных или монстров - все это надо увидеть.
Скупые строки биографии. Родился в 1898 году в Голландии. Учеба в школе архитектуры и орнамента в Гарлеме. Учителя, заметившие и оценившие большие способности юноши в графике. Десятилетнее пребывание в Риме. Затем в Швейцарии, Бельгии и, наконец, в голландском городе Барне. И в рамках этой неяркой внешними событиями жизни — драматическая история напряженных творческих поисков.
Его литографии, гравюры на дереве, меццо-тинто можно увидеть в кабинетах математиков и других ученых всего мира. Некоторые его работы носят жутковатый, сюрреалистический оттенок, но произведения Эшера - это не фантасмагория Сальвадора Дали или Рене Маргитта, а тонкие философские и математические наблюдения.
Творчество этого художника возбудило большой интерес со стороны математиков и физиков. В его графике оказались заложенными глубокие принципы симметрии, которые были известны лишь кристаллографам. Оказалось, что многие работы Эшера могут быть проанализированы математическими методами

Слайд 9

"Предел круга III"

Здесь представлен один из двух видов неевклидового пространства, описанных французским математиком Пуанкаре. Чтобы понять особенности этого пространства, представьте, что вы находитесь внутри самой картины. По мере вашего перемещения от центра круга к его границе ваш рост будет уменьшаться также, как уменьшаются рыбы на данной картине. Таким образом путь, который вам надо будет пройти до границы круга будет казаться вам бесконечным. На самом деле, находясь в таком пространстве вы на первый взгляд не заметите ничего необычного в нем по сравнению с обычным евклидовым пространством. Например, чтобы достичь границ евклидового пространства вам также необходимо пройти бесконечный путь. Однако, если внимательно присмотреться, то можно будет заметить некоторые отличия, например, все подобные треугольники имеют в этом пространстве одинаковый размер, и вы не сможете там нарисовать фигуры с четырьмя прямыми углами, соединенными прямыми линиями,

Слайд 10

РАЙ И АД – Предел круга 4

Фигуры ангелов и дьяволов, вплотную примыкая друг к другу, заполняют плоскость. При движении от центра гравюры к ее краю фигуры уменьшаются, превращаясь в бесконечное множество фигурок, невидимых невооруженным глазом на самом краю. Этот замечательный орнамент основан на вполне математической идее – известной из евклидовой модели неевклидовой гиперболической плоскости, придуманной Анри Пуанкаре. Диск разделен на 6 секций, где доминируют ангелы на черном фоне и дьяволы – на белом. Таким образом, рай и ад меняются местами 6 раз. В промежуточных, «земных» стадиях они подобны друг другу.

Слайд 11

МЕНЬШЕ И МЕНЬШЕ

Гравюра «Меньше и меньше» показывает типичный фрактальный объект. Самые известные фигуры во фрактальной геометрии. Эти рисунки построены по очень простому и экономичному правилу. Чтобы один компьютер передал другому свое произведение, достаточно сообщить только это правило. Естественно, тут же возникает идея «сжать изображение», то есть упаковать его в наиболее экономном виде, используя фрактальные алгоритмы, или применить такие подходы для создания шифров и кодов. В некоторых случаях это делается и с большим успехом.

Слайд 12

"ВОДОВОРОТЫ"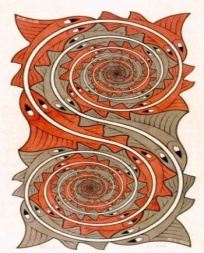

Эшер объединил спиралевидную форму и свой излюбленный художественный прием - регулярное разбиение плоскости (или мозаику). Здесь рыбы,выплыв из одного водоворота, попадают во второй и, погружась в него, постепенно уменьшаются в размерах и наконец совсем исчезают. Обратите внимание на постепенно уменьшающуюся в размерах мозаику. Если мысленно развернуть спираль, то мы увидим лишь два ряда рыб, плывущих навстречу друг другу. Но скрученные в спираль и соответствующим образом деформированные образы рыб полностью покрывают некоторую область бесконечной плоскости.

Слайд 13

ТРИ МИРА

Литография «Три мира» вызывает ощущение близости иной Вселенной. Вселенной, в которой существуют другие живые существа на Земле. Дело не только в том, что мы видим и слышим со многими из них в разных диапазонах. Не только в том, что «братья наши меньшие» могут иметь органы чувств, которых мы лишены. Представим хотя бы на минуту, что нашей естественной средой обитания была бы вода. Тогда земная твердь и океан в нашем восприятии как бы поменялись местами. Суша бы казалась чем-то вроде ближнего космоса. И, возможно, военные эксперты обсуждали бы вместо планов «звездных войн» возможности сухопутных боевых действий. Да и законы физики открывшись бы такой цивилизацией совсем в другом порядке

Слайд 14

Дата добавления: 2015-09-03