Комплексная форма ряда Фурье.

Ряд Фурье может быть также записан в комплексной форме, представив гармонические функции в виде суммы экспонент с мнимыми показателями, применив формулы Эйлера:

. (2.3)

Введем вместо a_n и b_n новые коэффициенты 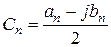для n= 1, 2, 3,¼ Величины C_n можно определить и при отрицательных индексах n, причем , поскольку коэффициенты a_n четны, а b_n нечетны относительно индексов. Таким образом, суммирование в (2.3) можно распространить на все значения n, положительные и отрицательные, включая и нуль:

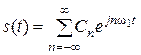, (2.4)

Формула (2.4) является рядом Фурье в комплексной форме. Коэффициенты ряда C_n находится по формуле

. (2.5)

Спектральная диаграмма периодического сигнала, представленного в форме (2.4), симметрична относительно начала отсчета частоты и содержит компоненты на отрицательной полуоси частот. Отрицательная частота – понятие не физическое, а математическое, обусловленное способом представления комплексных чисел. Рассмотрим тождество

Первое слагаемое в правой части изображается на комплексной плоскости вектором длины ½, который вращается с угловой скоростью w в направлении увеличения полярного угла w₁ t (рис.2.12), второе слагаемое изображается вектором, вращающимся в противоположном направлении. Складываясь, эти два комплексных числа дают вещественное число.

В ряде (2.4) слагаемые с положительными и отрицательными частотами образуют пары. Например,

.

При суммировании каждая пара дает соответствующую гармонику сигнала.

Спектры непериодических сигналов

Непериодический сигнал в ряд Фурье разложить нельзя. Для него вводят интеграл Фурье, который является пределом ряда, когда (T →∞).

Пусть s (t) – одиночный сигнал, длительность которого конечна. Дополнив его мысленно такими же сигналами, периодически следующими через некоторые интервалы времени T, мы получаем периодическую последовательность, которая может быть представлена в виде комплексного ряда Фурье (2.4).

Чтобы вернуться к одиночному импульсу следует устремить период к бесконечности. При этом:

1) основная частота следования w₁= 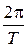→ 0. Это означает, что расстояние между спектральными линиями, равное основной частоте следования w₁, становится бесконечно малым и дискретная переменная n w₁ становится непрерывной w, сумма заменяется интегралом, спектр становится сплошным.

2) амплитуды гармонических составляющих 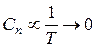, т.е. спектр состоит из гармонических составляющих с бесконечно малыми амплитудами.

Поэтому спектр непериодического сигнала характеризуется функцией спектральной плотности. Она показывает плотность распределения бесконечно малых амплитуд по оси частот, т.е. показывает, сколько гармонических составляющих с бесконечно малыми амплитудами приходится в диапазон частот df.

Функция спектральной плотности S (j ω) связана с сигналом s (t) через преобразование Фурье:

– прямое преобразование Фурье (ППФ). (2.6)

– обратное преобразование Фурье (ОПФ). (2.7)

Функция спектральной плотности – это комплексная функция частоты

S (j ω) = S (ω) e ^{j φ ( ω )} ,

где S (ω) – модуль функции спектральной плотности, его называют спектральной плотностью амплитуд,φ(ω) – аргумент функции спектральной плотности – спектр фаз.

Главной особенностью спектра непериодического сигнала является его сплошной непрерывный характер.

Пример. Найти S (j ω) одиночного прямоугольного импульса (рис. 2.13).

По временной диаграмме запишем аналитическое выражение такого сигнала:

Найдем функцию спектральной плотности импульса и приведем это выражение к функции типа (sin x / x).

Спектральная плотность амплитуд такого импульса (рис. 2.14) имеет вид:

.

Идеализированные модели сигналов часто имеют бесконечный спектр по оси частот. В то же время для них применяют понятие о ширине спектра, т.е. считают, что спектры у таких сигналов ограничены. Под шириной спектра понимают диапазон частот, в котором сосредоточена заданная доля от энергии всего сигнала, обычно 50%.

Для одиночного прямоугольного импульса за ширину спектра принимают интервал частот от 0 до 2p/τ_и, т.е. верхняя граничная частота спектра w_гр = 2p/τ_и..

Следовательно, чем короче импульс τ_и, тем шире его спектр w_гр.

2.4. Операторное представление сигнала

Преобразование Фурье применяется лишь для сигналов с конечной энергией, т. е. для сигналов, удовлетворяющих условию

.

Функция s (t), удовлетворяющая записанному условию, называется абсолютно интегрируемой.

Более универсальным является операторное представление сигнала, которое основано на преобразовании Лапласа. При операторном представлении сигналу s (t), как функции действительной переменной t, ставится в соответствие функция комплексной переменной р – S (p), где p = a + j ω (p называется комплексной частотой). Эта функция вводится следующим выражением, которое называется прямым преобразованием Лапласа (ППЛ):

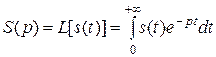(2.8)

Сигнал s (t) считается тождественно равным нулю при t < 0. Для существования этого интеграла сигнал s (t) должен иметь не более чем экспоненциальный степень роста при t > 0, т.е. должен удовлетворять неравенству | s (t)|£ k e ^at, где k, a – положительные числа. Тогда интеграл (5.3) сходится для всех комплексных чисел p, у которых Re(p) > a. Число a называется абсциссой абсолютной сходимости.

Сигнал s (t) называют оригиналом, а S (p) – изображением, или операторным представлением сигнала. Соответствие между изображением S (p) и оригиналом s (t) в сокращенной записи обозначается:

S (p) s (t)

По изображению можно восстановить оригинал обратным преобразованием Лапласа (ОПЛ):

. (2.9)

Интегрирование принято проводить по неограниченно протяженной вертикальной оси, располагающейся правее абсциссы абсолютной сходимости интеграла (2.8). В частном случае ограниченного сигнала можно положить с= 0.

Найдем изображения некоторых функций по формуле (2.8):

, d(t) 1; 1(t) 1/ p; A A / p (210)

, в частности, , . (2.11)

Записав sin(w t) и cos(w t) по формуле Эйлера через экспоненты и используя свойство линейности и формулы (5.8), получаем

, (2.12)

. (2.13)

Аналогично,

cha t , sha t . (2.14)

Для нахождения функции спектральной плотности S (j ω) по известному операторному представлению S (p) сигнала необходимо оператор р заменить на j ω, т.е. S (j ω) = S (р)| _{р = j ω}.

Пример. Найти спектральную плотность S (j ω) для единичной функции (рис. 2.15).

;

2.5. Свойства преобразований Фурье и Лапласа

Так как преобразования Фурье и Лапласа схожи, большинство их свойств совпадает. Рассмотрим эти свойства.

1). Свойство линейности. Для любых комплексных постоянных a и b, если (здесь и в дальнейшем) s ₁(t) ® S ₁(j ω), s ₂(t) ® S ₂(j ω), то

a s ₁(t)+b s ₂(t) ® a S ₁(j ω) + b S ₂(j ω), a s ₁(t)+b s ₂(t) a S ₁(p) + b S ₂(p).

Это вытекает из линейности преобразований Фурье и Лапласа.

2). Теорема запаздывания. Спектр сигнала, сдвинутый по оси времени на время t _з (время задержки), равен спектру исходного сигнала, помноженного на множитель :

s ₁(t – t _з) ® S ₁(j ω) , s ₁(t – t _з) S ₁(p)

На рис. 2.16 приведены сигналы: без временного сдвига (рис. 2.16, а), сигнал с задержкой на время t ₀ (рис. 2.16, б) и сигнал с опережением на время t ₀ (рис. 2.16, в). Напомним, однако, что при преобразовании Лапласа сигнал считается тождественно равным нулю при t < 0.

3). Теорема подобия. Изменение масштаба сигнала по оси времени приводит к изменению масштаба его спектра по оси частот

s ₁(α t) ® S ₁(j ω /α), s ₁(α t) S ₁(p /α).

Если α>1, то сигнал сжимается по оси времени, что приводит к растяжению его спектра по оси частот.

Если 0<α<1, то сигнал растягивается по оси времени, а его спектр сжимается по оси частот.

Пример: s ₁(t) = cos(ω t); s ₂(t) = cos(2ω t).

4) Дифференцирование сигнала эквивалентно умножению его спектра на множитель j ω (или изображения на p).

d (s ₁(t))/ dt ® j w S ₁(j ω), d (s ₁(t))/ dt p S ₁(p)– s ₁(0).

При дифференцировании выделяются высокочастотные составляющие спектра сигнала, а низкочастотные ослабляются, так как имеют малый масштабный множитель.

Изображения производной по Лапласу содержит начальное значения функции в отличие от преобразования Фурье.

5) Интегрирование сигнала эквивалентно умножению спектра на множитель 1/ j ω.

,

При интегрировании выделяются низкочастотные составляющие, а высокочастотные подавляются.

2.7. Мощности сигнала

При рассмотрении энергетических процессов в электрических цепях пользуются следующими понятиями о мощности сигнала.

1. р (t) = dW (t) /dt – мгновенная мощность – скорость изменения энергии W,потребляемой участком цепи. Для электрических цепей она рассчитывается по выражению:

p (t) = u (t) i (t).

Если р > 0, участок электрической цепи поглощает энергию, энергия возрастает, такой участок называется пассивным; если р < 0, участок электрической цепи выделяет (создает) энергию, отдавая ее во внешнюю цепь, такой участок называется активным.

2. Энергия – мощность сигнала за временной интервал t₂ – t₁:

= = = .

3. Средняя мощность – это энергия в единицу времени, т.е. Р _ср = W /(t₂ – t₁).

Для периодического сигнала средняя мощность рассчитывается так:

P _ср = .

4. Для удобства расчета в цепях переменного тока вводят понятие о действующих значениях напряжения или тока:

; .

Действующее значение переменного во времени напряжения или тока численно равно такому значению постоянного во времени напряжения или тока, которое выделяет мощность, равную средней мощности переменного сигнала за период.

Действующие и амплитудные значения гармонических напряжений и токов связаны соотношением:

; .

5. Мощности цепи гармонического тока.

Пусть через участок цепи (рис. 2.17) протекает гармонический ток i (t) = I_m cos(w₀ t +j _i).При этом на нем возникает напряжение u (t) = U_m cos(w₀+j _u).

Тогда мгновенная мощность определяется выражением

p (t) = i (t) U (t) = 1/2 U_mI_m cos(j _u – j _i) + 1/2 U_mI_m cos(2w₀ t + j _u –j _i).

Она состоит из двух слагаемых. Второе зависит от времени и изменяется с частотой в 2 раза выше, чем ток или напряжение на этом участке цепи, а первое от времени не зависит, его называют средней мощностью. Оно зависит от сдвига фаз между напряжением и током. Когда мгновенная мощность отрицательна, а это имеет место (см. рис. 2.22), когда u и i разных знаков, т.е. когда направления напряжения и тока в двухполюснике противоположны, энергия возвращается из двухполюсника источнику питания. Такой возврат энергии источнику происходит за счет того, что энергия периодически запасается в магнитных и электрических полях соответственно индуктивных и емкостных элементов, входящих в состав двухполюсника.

В цепях гармонического тока пользуются следующими мощностями:

1. Среднее значение мгновенной мощности (активная мощность) Р_A:

Р_А = 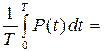UI cos(j _u – j _i);

φ = j _u – j _i – фазовый сдвиг между током и напряжением.

Активная мощность р_А максимальна, когда ток и напряжение находятся в одной фазе φ = 0,т.е. j _u = j _i.

Активная мощность выделяется (поглощается) на участке цепи, совершая полезную работу, превращаясь в тепловую или механическую форму энергии.

Активная мощность измеряется в ваттах (Вт).

2. Реактивная мощность

P_Q = UI sin(j _u – j _i).

P_Q характеризует энергию, которая накапливается реактивными элементами цепи и возвращается затем в цепь. P_Q иногда называют «кажущаяся» мощность т.к., P_Q не потребляется участком цепи и не выполняет никакой работы.

Реактивная мощность измеряется в варах (Вар – вольт-ампер реактивный).

3. Полная мощность

P_s = .

Величину cos j = P_A/P_s называют коэффициентом мощности, который показывает, какая доля от P_s совершает полезную работу, т.е. является активной мощностью (P_A). Фактически это кпд участка цепи, например электродвигателя.

Полная мощность измеряется в ВА (вольт-ампер).

4. Комплексная мощность. Активную, реактивную и полную мощности можно определить, пользуясь комплексными изображениями напряжения и тока. Пусть , а . Тогда комплекс полной мощности:

где I * - комплекс, сопряженный с комплексом .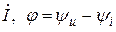

2.8. Распределение мощности в спектре периодического сигнала

Пусть s (t) – ток, напряжение (произвольная периодическая функция времени).

Разложим в ряд .

Вычислим среднюю мощность за период при R _н =1Ом:

.

Возведем в квадрат, получим слагаемые следующего вида:

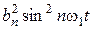
1) ; 2) ; ; 3) .

После интегрирования за период получим 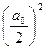, и . Все интегралы от гармонических функций за период обратятся в ноль.

Отсюда получим, что средняя мощность периодического сигнала равна

.

Полная мощность является суммой средних мощностей, выделяемых по отдельности постоянной составляющей и гармониками периодического сигнала.

Контрольные вопросы

1. Записать комплексную амплитуду гармонического напряжения u (t) = 311cos(2π100 t –π/4).

2. Записать выражение для гармонического напряжения с частотой 150 Гц, комплексная амплитуда которого u = 100 e ^{– j π/4}.

3. Какой сигнал называется дискретным?

4. Какие сигналы способны (без преобразований) нести полезную информацию?

5. Какой характер имеет спектр периодического сигнала?

6. Что происходит со спектром сигнала по оси частот при изменении масштаба сигнала по оси времени в a > 1 раз?

7. Что понимают под шириной спектра сигнала?

8. Какие составляющие сигнала ослабляются при его интегрировании и дифференцировании?

9. Что собой представляют действующие значения переменного тока либо напряжения?

Дата добавления: 2015-09-02