Сейсмическая миграция

Сейсмические временные разрезы, строящиеся в системе координат x,t₀, рассматриваются как изображение среды. Такое допущение основано на отождествлении времени пробега волны с глубиной залегания границы. Это возможно в том случае, когда направление лучей близко к вертикальному (при квазигоризонтальном залегании границ) и точки регистрации отраженных волн проецируются в точки отражения.

При наклонном залегании слоев происходит смещение точек отражения в направлении восстания границ (сейсмический снос, миграция) и временной разрез отображает геологический с искажениями: выполаживание наклонных границ, неоднозначность прослеживания волн, отраженных от криволинейных поверхностей («петли», «заходы»). Для исправления этих искажений применяется миграционное преобразование сейсмических волновых полей и прежде всего – при построении глубинных разрезов по материалам МОВ. Эта процедура в практике обработки получила название «миграция».

Миграционное преобразование в графическом виде было реализовано уже на ранних этапах развития метода в виде способов перестроения годографов отраженных волн в отражающие границы (способ окружностей, способ эллипсов, лучевые диаграммы второго рода и т.п.).

С внедрением в практику сейсморазведки обработки материалов на ЭВМ был разработан ряд алгоритмов миграционного преобразования. Их можно классифицировать по следующим признакам.

1. По способу описания среды:

- алгоритмы, основанные на среднескоростной аппроксимации разреза;

- алгоритмы, основанные на слоисто- однородной, слоисто-блоковой и т.п. (эти алгоритмы учитывают преломление сейсмических волн на промежуточных границах раздела но требуют их описания).

2. По способу описания волнового поля:

- во временной области;

- в частотной области.

3. По способу решения задачи миграционного преобразования:

- в лучевом приближении;

- путем решения скалярного волнового уравнения.

4. По виду исходной информации:

- временные разрезы;

- исходные (несуммированные) сейсмограммы ОПВ, ОПП, ОГТ.

4. По метрике пространства решений:

- двумерное изображение (мигрированные разрезы);

- трехмерное изображение («куб данных»).

Каждый из используемых алгоритмов характеризуется некоторой комбинацией признаков этой классификации.

В настоящее время наиболее распространенными являются алгоритмы, основанные на решении волнового уравнения во временной области, использующие среднескоростную аппроксимацию разреза. Среди них можно выделить:

- способы миграционного преобразования, основанные на решении скалярного волнового уравнения, , где l,m - коэффициенты Ламе, - вектор смещения, компонентами которого являются u(x),v(y),w(z), s - плотность среды, 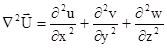- дифференциальный оператор Лапласа. В результате решения в нижнем полупространстве строится изображение границ в виде динамического разреза, где интенсивность сигналов пропорциональна коэффициентам отражения в соответствующих точках границ. В настоящее время используются алгоритмы, основанные на решении волнового уравнения с помощью интеграла Кирхгофа[1] (быстрое преобразование Кирхгофа (БПК), С.А.Васильев), способом конечных разностей (СКР, Klaerbout D.F.)

- дифракционное преобразование (D-преобразование, Ю.В.Тимошин), основой которого является представление, базирующееся на принципе Гюйгенса-Френеля, о границе, как о совокупности точек, излучающих элементарные сферические волны, описываемые уравнениями дифрагированной волны;

Упомянутые алгоритмы ввиду значительной времяемкости оперируют с временными разрезами, результаты, полученные с их помощью, различаются между собой по разрешенности записи и уровню шума процедуры.

В качестве примера рассмотрим двумерное дифракционное преобразование временного разреза ОГТ в мигрированный временной разрез (временной разрез со сносом).

Пусть F(t₀,x) – сейсмотрасса временного разреза ОГТ. Согласно принципу Гюйгенса-Френеля сигналы отраженных и дифрагированных волн можно рассматривать как результат суперпозиции элементарных волн, генерируемых каждой точкой отражающей границы при падении на неё прямой волны (кинематические характеристики этих волн совпадают с характеристиками дифрагированных): , где D – символ дифрагированной волны; x_d– х-координата точки дифракции; х_i - x-координата трассы временного разреза ОГТ; - средняя скорость в толще над отражающей границей.

Годограф дифрагированной волны описывается уравнением: , где t_z – вертикальное время.

Для вычисления j-той трассы временного разреза со сносом выбирается база суммирования (апертура суммирования, апертура). Для сейсмотрасс апертуры рассчитывается поле годографов дифрагированных волн (для заданной закономерности (t₀)), по которым производится суммирование сигналов на трассах апертуры (аналогично суммированию с вводом кинематических поправок в способе ОГТ). Точки дифракций имеют х-координату x_d=x_j, параметр t_z изменяется в окне обработки на величину шага дискретизации. Схематическое изображение вышеописанной процедуры приведено на рис. 1.

Очевидно, что квазисинфазное сложение сигналов будет происходить лишь в области касания годографов дифрагированных волн и годографа t₀ отраженной волны. Остальное поле сейсмограммы суммируется в случайной фазе, создавая шум процедуры. Уровень его прямо пропорционален количеству трасс в апертуре (последняя должна заведомо перекрывать интервал от формируемой трассы разреза со сносом до точки касания годографов). Для снижения шума процедуры используется умножение суммируемых трасс апертуры на весовую функцию (аподизация). Весовая функция имеет максимум в центре апертуры и монотонно убывает к ее периферии (см. рис.2).

Результаты суммирования трасс апертуры относят к её центральной трассе (x_j). Смещение апертуры вдоль оси х временного разреза позволяет формировать годограф t_z отраженной волны.

Применение миграционного преобразования позволяет ликвидировать неоднозначность прослеживания волн на временных разрезах t₀ («петли», «заходы», искажение наклона границ и т.п.), упрощает волновую картину и, следовательно, повышает её достоверность (см. рис.3).

В последнее время усиленно разрабатываются алгоритмы миграции в частотной области (С.В.Бирдус, Ю.В.Тимошин), на базе которых реализованы программы, учитывающие преломление на промежуточных границах, и программы, работающие в трехмерном пространстве.

Кроме того, в комплексе программ параметрической обработки сейсморазведочной информации (SWAP, Ю.Н.Воскресенский, Е.Б.Варов) реализована лучевая миграция, опирающаяся на среднескоростную аппроксимацию разреза. Вследствие экономичности по затратам машинного времени оказывается возможным миграционное преобразование над исходными сейсмограммами ОПВ, ОПП, которые подвергаются дальнейшей обработке.

Литература

1. Знаменский В.В. Общий курс полевой геофизики. Учебник для вузов. – М.: Недра, 1989. – С. 455 – 467.

2. Клаербоут Д. Теоретические основы обработки геофизической информации с приложением к разведке нефти. Пер. с англ. – М.: Недра, 1981. – С. 266-267

3. Клаербоут Д. Сейсмическое изображение земных недр. Пер. с англ. – М.: Недра, 1989. – 407 с.

4. Козлов Е.А. Миграционное преобразование в сейсморазведке. – М.: Недра, 1986. 247 с.

5. Мешбей В.И. Методика многократных перекрытий в сейсморазведке. – М.: Недра, 1985. – С. 199 – 222.

6. Сейсморазведка. Справочник геофизика. /Под ред. И.И.Гурвича, В.П.Номоконова. – М.: Недра 1981. – С. 356 – 363.

Рис.1 Схема формирования трасс мигрированного временного разреза

Рис.2 График аподизационной функции.

Рис.3 Временной разрез t₀ (вверху), мигрированный временной разрез (внизу).

[1] Если источники сейсмических колебаний заключены в замкнутую поверхность S и известны значения компонент вектора смещений и их нормальные производные , то дифракционный интеграл Кирхгофа позволяет вычислить значения смещений в любой точке Р, лежащей вне объёма, ограниченного поверхностью S. Так, для компоненты u в изотропной среднескоростной модели среды со скоростью v_m можно записать , где u(P,t) – поле однократно отраженных и дифрагированных волн, R – расстояние от точки Р до всех точек поверхности S, t – момент прихода волны (для однородной среды t=R/v_m).

Дата добавления: 2015-08-21