По частным критериям

Наибольшая трудность анализа любого крупного технического и народнохозяйственного проекта заключается внеобходимости решения задачи многокритериальной оптими­за­ции для управления его характеристиками. При этом многокритериальную задачу желательно свести к однокритериальной задаче, сформулировав единую цель при множестве критериев:

.

Однако математика не может на это дать однозначного ответа (добиться оптимизации всех критериев одновременно невозможно в принципе), но может помочь принять решение и сделать правильный выбор. Реально возмож­но достичь только некоторого компромисса (сочетания требуемых ка­честв). В некоторых случаях эффективным методом сведения многокритериальной задачи к однокритериальной является расстановка приоритетов. В этом случае в многокритериальной задаче оптимизации на множестве допустимых решений задаются лексикографические отношения предпочтения: все критерии можно ранжировать (строго упорядочить) по важности так, что при последовательном рассмотрении критериев вначале используется первый критерий, затем второй и т.д. Задание набора ранжированных критериев 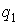, ,…, при синтезе сложной системы позволяет выделить некоторые стратегии в качестве оптимальных, упорядочить все стратегии по степени их предпочтительности (так располагают слова в словаре) и свести многокритериальную задачу к лексикографической [1].При отсутствии случайных и неопределенных факторов (детерминированной) в лексикографической задаче каждой стратегии соответствуют определенные числовые значения частных критериев. Оптимизация структуры и свойств сложной системы, состоящей из взаимосвязанных подсистем, находящихся на разных иерархических уровнях, легко представляется в лексикографической форме.

Как уже отмечалось, при сравнении двух стратегий в первую очередь используется первый критерий: лучшей считается та стратегия, для которой значение этого критерия больше. Если значения первого критерия для обеих стратегий равны, то применяется второй критерий и предпочтение отдается той стратегии, для которой его значение больше. Если и второй критерий не позволяет выделить лучшую стратегию, привлекается третий и т.д.

Лексикографическое отношение предпочтения задается в виде:

- стратегия предпочтительнее стратегии v (обозначается ), если выполняется одно из 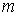условий:

1. ;

2. , ;

…

r. , ,…, , ;

…

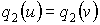m. , ,…, , .

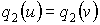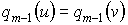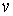- стратегии и v эквивалентны ( ~ ), если

, ,…, .

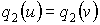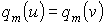- стратегия лексикографически не хуже (не менее предпочтительна), чем стратегия 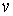(обозначается ), если выполнено одно из приведенных выше ( 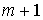) условий.

Отметим, любые две стратегии и v сравнимы по рассматриваемому отношению предпочтения, то есть всегда выполняется одно из условий

; ; ~ .

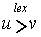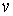В общем случае эффективность стратегии в рамках используемой модели характеризуется множеством чисел , отражающим степень достижения цели операции при использовании этой стратегии.

В лексикографической задаче оптимизации добиваются сколь угодно малого приращения более важного критерия за счет любых потерь по остальным менее важным критериям.

Лексикографически оптимальной будет стратегия 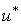, которая не хуже любой другой стратегии 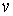, если .

При наличии лишь одного критерия эффективности оптимальная стратегия 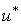определяется из условия ; - множество всех стратегий.

При решении лексикографической задачи оптимизации определяются оптимальные стратегии. Так как все такие стратегии эквивалентны, можно ограничиться отысканием не всего множества , а лишь одной оптимальной стратегии. Каждый последующий частный критерий сужает множество стратегий, получаемых с помощью всех предыдущих частных критериев:

.

Отметим, если в исходной задаче оптимизации с одним скалярным критерием имеется несколько решений, и для дальнейшего выбора последовательно применяются дополнительные критерии, то полученные в результате стратегии будут оптимальными для соответствующей лексикографической задачи с векторным критерием, состоящим из всех поочередно использовавшихся критериев.

В заключение отметим, решение большинства задач однокритериальной оптимизации позволяет получить однозначное решение. В задачах жемногокритериальной оптимизации при переходе от одного варианта к другому, как правило, улучшаются значения одних критериев, но ухудшаются значения других. Компромисс разрешается введением тех или иных дополнительных ограничений или субъективных предположений. Здесь нельзя говорить об объективном единственном решении задачи; выбор наилучшего решения в значительной степени субъективен. Так как область допустимых решений очередной задачи представляет собой множество оптимальных решений предшествующих задач, то она быстро сужается до одной точки, лишая свободы выбора при максимизации последующих критериев. Следует помнить, что решение задачи оптимизации существенно зависит от результатов ранжирования критериев качества. В известной мере избавиться от этого недостатка позволяет применение метода последовательных уступок, процедура которого включает:

- расположение частных критериев в порядке их относительной важности;

- максимизацию первого, наиболее важного критерия; назначение величины допустимого снижения (уступки) значения этого критерия;

- максимизацию второго по важности частного критерия при условии, что значение первого критерия не должно отличаться от максимального более, чем на величину уступки;

- назначение величины уступки по второму критерию;

- максимизацию третьего критерия при условии, чтобы значения первых двух критериев не отличались от ранее найденных максимальных значений больше, чем на величины соответствующих уступок и т.д.

Здесь многокритериальная задача сводится к поочередной максимизации частных критериев и выбору величин уступок (чем уступки меньше, тем приоритет жестче); оптимальной считается любая стратегия, соответствующая условному максимуму последнего по важности критерия.

Приведенный метод широко и эффективно нами использовался при решении задач управления в технических системах разной направленности (формирование управляющих воздействий оператора эргатической системы, оценка имитационных характеристик тренажных и обучающих комплексов, оптимизация рецептурно-технологических параметров композиционных материалов, моделирование задач гемодинамики в сердечно-сосудистой хирургии и т.д.).

Определение Задача многокритериальной оптимизации формулируется следующим образом: где это k () целевых функций. Векторы решений относятся к не пустой области определения S. Задача многокритериальной оптимизации состоит в поиске вектора целевых переменных, удовлетворяющий наложенным ограничениям и оптимизирует векторную функцию, элементы которой соответствуют целевым функциям. Эти функции образуют математическое описание критерия удовлетворительности и, как правило, взаимно конфликтуют. Отсюда, «оптимизировать» означает найти такое решение, при котором значение целевых функций были бы приемлемыми для постановщика задачи. Эталонные точки Для возможности оценки качества найденных решений, обычно рассматривают такие точки в области значения целевой функции: идеальная точка, Y I, утопическая точка, Y U, надир (надир), Y N. В некоторых случаях эти точки могут быть решениями. Идеальная точка определяется как вектор, каждая из координат которого имеет оптимальное значение соответствующей составляющей целевой функции: Точка надир определяется как вектор: Утопическую точку Y U вычисляют на основе идеальной: где?> 0, U - единичный вектор. Критерии оптимальности Критерий Парето Вектор решения называется оптимальным по Парето если не существует такого, что для всех и для хотя бы одного i. Множество оптимальных по Парето решений можно обозначить как P (S). Целевой вектор является оптимальным по Парето, если соответствующий ему вектор из области определения также оптимальный по Парето. Множество оптимальных по Парето целевых векторов можно обозначить как P (Z). Множество оптимальных по Парето векторов является подмножеством оптимальных по Парето в слабом смысле векторов. Вектор является слабым оптимумом по Парето тогда, когда не существует вектора такого, что для всех. Диапазон значений оптимальных по Парето решений в области допустимых значений дает полезную информацию об исследуемой задачу если целевые функции ограничены областью определения. Нижние границы оптимальной по Парето множества представлено в «идеальном целевом векторе». Его компоненты Z и полученные путем минимазации каждой целевой функции в пределах области определения. Множество оптимальных по Парето решений также называют Парето-фронтом (англ. Pareto-frontier). Лексикографический порядок Если одни целевые функции важнее другие, критерий оптимальности можно определить с лексикографическим порядком. Отношение лексикографического порядка < lex между векторами и выполняется, если A Q < B Q, где. То есть, первые q компонент вектора меньше компоненты вектора, а компоненты q + 1 - уровни (если есть). Лексикографический порядок для случая действительных чисел является линейным. Вектор является лексикографическим решением, если не существует вектора такого, что. Поскольку отношение лексикографического порядка является линейным, можно доказать, что вектор является лексикографическим решением, если для всех выполняется: Основной особенностью решений по лексикографическим порядком является существование выбора между критериями. Лексикографическая упорядоченность требует ранжирования критериев в том смысле, что оптимизация по критерию F K возможна лишь тогда, когда был достигнут оптимума для предыдущих критериев. Это означает, что первый критерий имеет наибольший приоритет, и только в случае существования нескольких решений по этому критерию, будет поиск решений по второму и остальным критериев. Существование иерархии среди критериев, позволяет решать лексикографические задачи последовательно, шаг за шагом минимизируя за каждым следующим критерием, и использующие оптимальные значения предварительных критериев как ограничения. Скаляризация Для получения оптимальных по Парето решений часто используют методы скаляризации. Поскольку целевая функция задачи многокритериальной оптимизации имеет векторные значения, ее превращают в функцию со скалярным значением. Таким образом, задача многокритериальной оптимизации сводится к задаче оптимизации с одной скалярной целевой функцией. Функция скаляризации имеет удовлетворять следующим условиям. Пусть F - функция скаляризации, что превращает векторную функцию на скалярную. Если F сохраняет упорядоченность по Парето, то есть, если для произвольных выполняется: тогда решение, что минимизирует F на X является решением по Парето. Если F сохраняет отношение порядка < в, то есть, если для произвольных выполняется: тогда решение, что минимизирует F на X является слабым по Парето. Если F непрерывна на, и единственная точка минимума F на X, тогда является решением по Парето. Взвешенная сумма Приведенная функция F 1 сохраняет упорядоченность по Парето для w > 0. Поэтому решения, минимизирующие F 1 на X для произвольных w > 0 являются оптимальными по Парето. Однако F 1 не сохраняет упорядоченность по Парето для а сохраняет лишь отношение < и поэтому решения, минимизирующие F 1 на X для являются слабыми по Парето. Недостатком метода взвешенных сумм в случае выпуклой множества значений целевых функций является невозможность охватить все оптимальные по Парето точки из множества Парето-фронта. В задачах комбинаторной многокритериальной оптимизации множество целевых значений не является выпуклой, поэтому метод взвешенных сумм не подходит для скаляризации целевых функций для этих задач. Функция скаляризации Чебышева Взвешенная функция скаляризации Чебышева сохраняет отношения < и поэтому минимум является слабым по Парето. Метод изменения ограничений (?-ограничения) По методу изменения ограничений одну из целевых функций оставляют в качестве целевой, а остальные превращают в ограничения. То есть, пусть F R будет целевой, а остальные как ограничение неравенства: при условиях: Значение могут рассматриваться как допустимые уровни для Методы решения Интерактивность Часто, решения задачи многокритериальной оптимизации происходит с участием эксперта - человека, который выбирает и принимает решения на основе информации, представленной системой поддержки принятия решений. Возможно участие группы из нескольких экспертов. В случае участия человека в поиске решения алгоритмы и методы называют интерактивными. Эволюционные методы Упоминания о применении генетических алгоритмов для решения задачи многокритериальной оптимизации относятся к концу 1960-х.

Источник: http://life-prog.ru/view_optimization.php?id=2

Дата добавления: 2015-08-21