Конвективтік диффузияның дифференциалдық теңдеуі.

Конвективтік диффузия кезінде таралатын зат концентрациясы фазаның қарапайым көлемінде тек молекулалық диффузия көмегімен ғана емес, сонымен қатар, бір концентрациялық аймақтан екіншісіне механикалық жолмен берілуі нəтижесінде өзгереді. Бұл жағдайда таралатын зат концентрациясы координаталар x, y, z жəне τ функциясы ғана болып қоймай, сонымен қатар, элемент қозғалысының жылдамдығы wx, wy, wz

де функциясы болады. Конвективтік диффузияның дифференциалдық теңдеуі массаалмасудың тұрақталған үдерісінде берілген компоненттің қозғалыстағы ортадағы концентрациясының таралуын көрсетеді:

15. Молекулалық диффузияның дифференциалдық теңдеуі (Фиктің екінші заңы). Молекулалық диффузияныңдифференциалдық теңдеуі қозғалыссыз ортада немесеқозғалыстағы ламинарлық ағындағы массаалмасудыңтұрақталмаған үдерісін сипаттайды

19. Сұйық пен бу жүйелеріндегі фазалық тепе-теңдік. Егер сұйық бинарлы қоспаны қандай да бір уақытқа, температура мен қысымды тұрақты қылып оқшауланған ортада қайнатса, ол жүйеде тепе-теңдік орнайды. Идеалдық қоспалар Рауль заңына бағынады.

Мұндағы P^п_А ,P ^п_В– А мен В компоненттерінің парциалдық қысымы; х,(1–х) –олардың сұйық қоспадағы мольдік үлестері; РА,РВ – таза компоненттердің буларының қысымы. Жүйедегі компоненттердің парциалдық қысымы Дальтон заңына бағынады.

мұндағы Р – жүйедегі жалпы қысым; у, (1–у) – бу қоспасындағы А мен В-ның мольдік үлестері. Тұрақталған тепе-теңдік үшін

Осыдан

Негізінен ректификация үдерісін изобаралық жағдайда өткізеді, сондықтан идеалдық бинарлы қоспаны P=const кезінде қарастырамыз. (3.2) теңдікті х-қа байланысты шешеміз, яғни

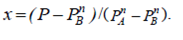
P ^п_А мен P^п _Вмəндерінің қайнау температуралары tкА жəне tкВ кезінде белгілі болса, онда (3.57) теңдеуінен х – сандық мəнін, ал (3.56)-дан у – сандық мəнін табуға болады. Осыдан температураны біле отырып жəне жоғарыда

есептеліп алынған х пен у-тің сандық мəндері арқылы жүйедегі тепе-теңдікті сипаттайтын диаграмманы тұрғызамыз (3.4-сурет). Осы диаграммадан х сұйық фазасының құрамына сəйкес, тепе-теңдігі бу у-тің құрамын жəне жүйедегі температураны табуға болады. Бұл y*=f(x) үшін мынадай тепе-теңдік теңдеуіне сəйкес келді.

Егер деп алсақ, α – А компонентінің салыстырмалы ұшқыштығы деп аталады Онда

жəне 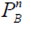мəндері tkA мен tkB аралығында тұрақты болмайды, сондықтан қарапайым есептеуде α-ның орташа сандық мəнін алады.

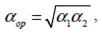
мұндағы α1 мен α2 температуралар tkA мен tkB кезіндегі

салыстырмалы ұшқыштықтар

Дата добавления: 2015-08-21