Методические указания. «кривые и поверхности второго порядка»

ТИПОВОЙ РАСЧЕТ

«КРИВЫЕ И ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА»

Для студентов дневной формы обучения

специальности 072500 «Дизайн»

Составитель: доцент кафедры высшей математики, к.т.н Н.С. Кривша

Методические указания

Типовой расчет содержит пять заданий.

1. Выполнение первого задания было разобрано на лекции.

2. Выполнение второго задания требует знания канонических уравнений кривых второго порядка и уравнения прямой линии на плоскости.

Решим типовую задачу.

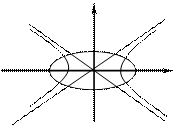
Задача 1. Фокусы эллипса совпадают с фокусами гиперболы 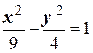. Эллипс проходит через точку . Составить уравнение этого эллипса.

Решение. Обозначим через 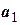и полуоси данной гиперболы, через 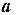и - полуоси искомого эллипса. Имеем 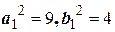, откуда 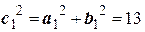. Так как фокусы эллипса совпадают с фокусами данной гиперболы, то и для эллипса 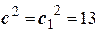. Уравнение эллипса ищем в виде 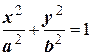. Так как точка принадлежит эллипсу, то ее координаты удовлетворяют уравнению эллипса и, кроме того, выполнено соотношение 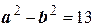. Таким образом, для определения 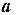и имеем систему:

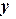
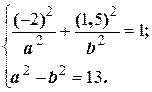
Обозначив и ,

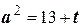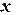получим

Решая, находим (рис.1).

Ответ: . Рис.1

3. В третьем задании требуется привести к каноническому виду уравнение кривой второго порядка, выполнив последовательно поворот, а затем параллельный перенос координатных осей.

Задача 2. Дано уравнение кривой второго порядка 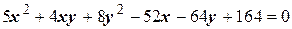. Выполнив поворот и параллельный перенос координатных осей, получить каноническое уравнение кривой и построить ее в исходной системе координат.

Решение. Выполняем поворот осей по формулам ; 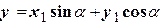. Подставим эти выражения для 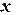и 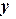в исходное уравнение и выделим коэффициент при :

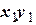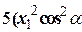
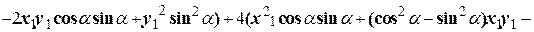
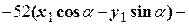
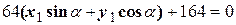(1)

Приравняв к нулю коэффициент при 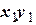, получаем:

,

откуда .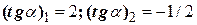

Зная 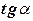, можно найти и по формулам тригонометрии:

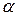Если угол поворота условиться считать острым, то в этих формулах надо брать знак плюс, и для 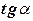надо взять также положительное решение. Выберем, например, угол поворота , найдем , подставим их в (1). После вычисления коэффициентов получим уравнение:

.

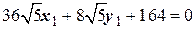В полученном уравнении выделим полные квадраты двучленов

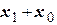и :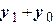

.

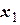
Выполнив параллельный перенос

по формулам , ,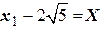

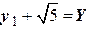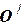получим в системе уравнение кривой

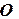
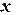
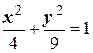: это эллипс с полуосями

2 и 3 соответственно (рис.2). Рис. 2

4. Выполнение четвертого задания предполагает знание уравнений прямой на плоскости и в пространстве и уравнений плоскости.

Решим типовую задачу.

Задача 3. Провести плоскость через перпендикуляры из точки 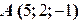к плоскостям и . Найти расстояние от основа­ния первого перпендикуляра до второй плоскости.

Решение.

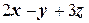
1. Обозначим через первую плоскость , а через - вторую плоскость . Очевидно, что в качестве нормаль­ного вектора 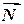искомой плоскости можно взять векторное произведе­ние нормальных векторов и 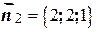данных плоскостей и :

.

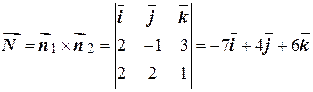Теперь, используя уравнение плоскости, проходящей через данную точку 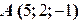перпендикулярно вектору 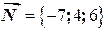, получаем 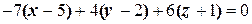или .

2. Найдем проекцию P точки 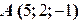на плоскость . Вектор будет направляющим вектором перпендикуляра AP, то есть

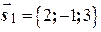. Поэтому каноническое уравнение этого перпендикуляра имеет вид

.

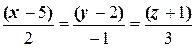Приводим данные уравнения к параметрическому виду, приравнивая к 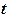каж­дое из трех данных отношений: .

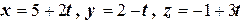Подставляя полученные значения 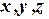в уравнение плоскости :

, получаем: , откуда находим значение параметра, соответствующее точке P пересечения прямой AP с данной плоскостью .

Находим координаты P:

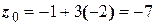,то есть .

3.Используя формулу расстояния от точки P до плоскости , находим:

.

Ответ: искомая плоскость , а расстояние от основания перпендикуляра AP на плоскость до плоскости равно 5/3.

5. Пятое задание предлагает изобразить тело, ограниченное заданными поверхностями второго порядка и плоскостями.

Решим конкретную задачу.

Задача4. Нарисовать тело, ограниченное указанными поверхностями. Указать тип поверхностей, ограничивающих данное тело:

.

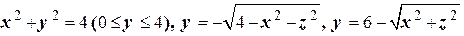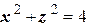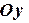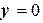Решение. В плоскости уравнение задает окружность радиуса 2 с центром в начале координат. В пространстве этому уравнению соответствует цилиндрическая поверхность, образующие которой параллельны , а направляющей служит вышеупомянутая окружность. Неравенство указывает, что берется часть этой поверхности, ограниченная плоско­стями и .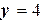

Рассмотрим уравнение . Возведя в квадрат левую и пра­вую части, получим 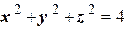. Это сфера радиуса 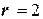с центром в начале координат. Значит, уравнение задает левую половину сферы.

Наконец, уравнение 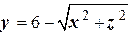преобразуем так:

.

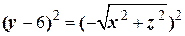Будет 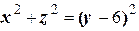- это конус

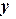
с вершиной в точке ,

вытянутый вдоль оси .

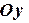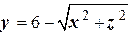Уравнение задает

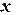левую его часть.

Рис.3

А теперь только остается нарисовать тело, ограниченное рассмотренными поверхностями (рис.3).

Дата добавления: 2015-08-21