Краткая теория

МИНИСТЕРСТВО ТРАНСПОРТА РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ГРАЖДАНСКОЙ АВИАЦИИ

__________________________________________________________________________________________

В.А.Курочкин

ЛАБОРАТОРНАЯ РАБОТА

ПО ФИЗИКЕ В - 4

ДИФРАКЦИЯ ФРАУНГОФЕРА

Москва 2012

ДИФРАКЦИЯ ФРАУНГОФЕРА

Лабораторная работа В-4

Цель работы

Изучение явления дифракции света, экспериментальное исследование дифракционной картины от узкой щели, опытное определение длины волны лазерного излучения.

Подготовка к работе

Изучите теоретический материал по учебникам [1]-[3]: явление дифракции, особенности дифракции Фраунгофера и Френеля, принцип Гюйгенса-Френеля, метод зон Френеля, условия минимумов и максимумов интенсивности на дифракционной картине от узкой щели. Ознакомьтесь с устройством лабораторной установки. Подготовьте ответы для допуска к лабораторной работе.

Краткая теория

Дифракция света - совокупность явлений, наблюдаемых при распространении световых волн в среде с резкими неоднородностями.

При падении плоской монохроматической волны на узкую щель в непрозрачной преграде на удалённом экране наблюдается дифракционная картина с характерным чередованием светлых и тёмных полос- максимумов и минимумов интенсивности I -при этом свет как бы огибает края щели, проникая в область геометрической тени (рис.1).

При достаточно больших расстояниях L от щели до экрана лучи, идущие в определённую точку экрана, можно считать параллельными – в этом случае говорят о дифракции Фраунгофера; ди фракция в непараллельных лучах носит название дифракции Френеля.

Условия дифракции Фраунгофера можно также выполнить, поместив за щелью собирающую линзу и разместив экран в её фокальной плоскости (рис.2). В этом случае каждой точке экрана будет соответствовать система параллельных лучей, падающих на линзу под определённым углом φ к её оптической оси (этот угол называют углом наблюдения; F - фокусное расстояние линзы).

Для анализа явления дифракции используется принцип Гюйгенса- Френеля. Согласно этому принципу:

1. Открытый участок волнового фронта представляется в виде множества малых элементов - вторичных когерентных источников.

2. Волновой фронт за препятствием является поверхностью, огибающей волновые фронты вторичных волн.

3. Распределение интенсивности света в зоне дифракции является результатом интерференции вторичных волн, приходящих от вторичных источников в точки наблюдения.

Полный расчёт функции I(x) вдоль экрана требует сложения волн от большого

(в пределе – бесконечного) количества вторичных источников.

В случае, если нас интересуют только положения максимумов и минимумов на дифракционной картине - эти расчёты можно упростить, воспользовавшись методом зон Френеля.

Согласно этому методу открытую часть волнового фронта в плоскости щели следует разбить на зоны (по сути, - группы вторичных источников) в виде полос, параллельных краям щели. При заданном угле наблюдения ширина каждой зоны a выбирается так, чтобы разность хода лучей, приходящих в точку наблюдения от краёв зоны, равнялась 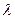/2. При таком выборе зон колебания, возбуждаемые на экране вторичными волнами от краёв двух соседних зон, оказываются в противофазе и гасят друг друга.

На рис.3 показан случай, когда на ширине щели укладываются две зоны Френеля - AB и BC. Согласно методу Френеля разности хода лучей, идущих от краёв зон в точку наблюдения под углом , равны:

BF= CG= a sin = 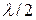(1)

Условие (1) выполняется также для любых пар вторичных источников, отстоящих от точек A и B (например, для середин зон D и E). В итоге две соседние зоны, показанные на рис. 3, дадут на экране интенсивность света I= 0. Очевидно, что таким же будет результат и для любого чётного количества N зон Френеля: N=2m (m= 1, 2, 3,……).

Умножая обе части равенства (1) на 2 m и учитывая, что Na=b (b- ширина щели), получим следующее условие минимумов интенсивности на дифракционной картине:

(m= 1, 2, 3,……) (2)

В формуле (2) число m носит название порядка минимума,а знаки «+» и «-» отражают симметричность расположения минимумов относительно центра дифракционной картины (точки 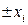на рис. 2).

В случае, если общее количество зон Френеля на ширине щели будет нечётным (N= 2 m+ 1; m= 1, 2, 3,……), то колебания одной из зон окажутся нескомпенсированными. Этот случай соответствует условию максимума:

(m= 1, 2, 3,…….) (3)

В центральной точке дифракционной картины, наблюдаемой под углом φ=0, располагается наиболее интенсивный центральный максимум, соответствующий взаимному усилению всех вторичных волн с нулевым сдвигом по фазе.

Необходимо подчеркнуть, что размеры зон Френеля и их количество на ширине щели зависят от угла наблюдения ; при этом число N будет целым (чётным или нечётным) только для точек минимумов или максимумов.

При удалении от центра дифракционной картины интенсивность I резко падает. В связи с этим реально удаётся наблюдать минимумы сравнительно невысоких порядков, для которых углы φ очень малы. Учитывая это, можно записать (см. рис. 2):

, (4)

где - модуль координаты минимума порядка m в фокальной плоскости линзы, F- фокусноерасстояние линзы. Выражая из формулы (2) sin φ, получаем следующее выражение для координат дифракционных минимумов на экране:

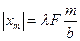. (5)

Дата добавления: 2015-08-21