Ланцюг з двох розпадів

Тепер розглянемо випадок з двох розпадів у ланцюзі: один нуклід A розпадається в інший B, тоді B розпадається ще в наступний C, тобто A → B → C. Попереднє рівняння не можна застосувати до ланцюгу розпадів, але його можна узагальнити. Оскільки A розпадається в B, тоді B розпадається в C, активність речовини A додає нукліди B, до того як ці нукліди речовини B розпадуться. Інакше кажучи, кількість ядер речовини другого покоління B збільшується у висліді розпаду речовини A і зменшується внаслідок власного розпаду в речовину третього покоління C. ^[3] Сума цих двох доданків і дає закон для ланцюгу розпаду для двох нуклідів:

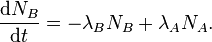
Швидкість зміни N_B, яка є d N_B /d t, стосується змін кількості A і B, N_B може зростати оскільки B утворюється з A і убувати оскільки B утворює C.

Переформулювання із використанням попередніх результатів:

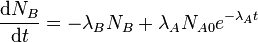
Нижні індекси просто вказують на відповідні нукліди, тобто N_A це кількість нуклідів типу A, N_{A 0} це початкова кількість нуклідів типу A, λ_A це стала розпаду для A — і схоже для нукліду B. Розв'язання рівняння для N_B дає:

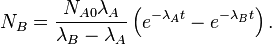
Природно, це рівняння зводиться до попереднього у випадку якщо B є стабільним нуклідом (λ_B = 0):

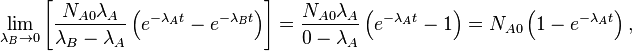
як показано вище для одиночного розпаду. Розв'язок можна знайти через використання інтегрувального множника, де інтегрувальний множник є e ^λ _B^t і потім взяти визначений інтеграл від до

Дата добавления: 2015-08-21