Метод контурных токов, метод узловых потенциалов.

Задание {{87}}

Собственное сопротивлении второго контура равно

¨ R₁

¨ R₁+ R₂- R₃

x R₁+ R₂ + R₃

¨ R₁+ R₂

Задание {{88}}

Собственное сопротивлении первого контура равно

¨ R₁

¨ R₁+ R₂- R₃

x R₄+ R₅ + R₃

¨ R₁+ R₂

Задание {{89}}

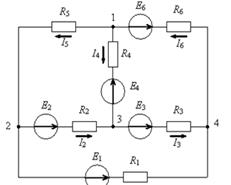
Общая проводимость для второго и третьего узла равна

¨ 1/R₃

¨ 1/R₂ - 1/R₃

¨ 1/R₂ +1/R₃

x 1/R₂

Задание {{90}}

Общее сопротивление первого и третьего контура равно

¨ R₁+R₂

¨ R₁

¨ R₃

x R₅

Задание {{91}}

Общая проводимость для первого и третьего узла равна

¨ 1/R₁-1/ R₃

x 1/ R₃

¨ 1/R₁

¨ 1/R₁+1/ R₃

Задание {{92}}

Собственная проводимость четвертого узла равна

¨ 1/R₁ -1/ R₂ +1/R₆

¨ 1/ R₂

¨ 1/R₁

x 1/R₁+1/ R₂ +1/R₆

Задание {{93}}

Для представленной цепи общее сопротивление для второго и первого контура R₁₂ равно

¨ R₂

¨ R₁+ R₂

x R₄

¨ R₁

Задание {{94}}

Для представленной цепи собственное сопротивление первого контура R₁₁ равно

¨ R₂ + R₅

x R₂+ R₄ + R₅

¨ R₂- R₄ + R₅

¨ - R₂+ R₄ - R₅

Задание {{95}}

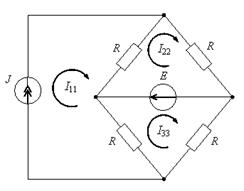
Если контурный ток I₁₁=4 A, ЭДС источника E = 20 В, а сопротивление резистора R = 5 Ом, то ток источника тока J равен

¨ 8

x 4

¨ 0

¨ -8

Задание {{96}}

Для представленной цепи собственная проводимость первого узла вычисляется по формуле

¨

¨ 0

¨ 2/R

x 3/R

Задание {{97}}

Если ток источника тока J = 5 А, ЭДС источника E = 12 В, а сопротивление резистора R = 4 Ом, то контурный ток равен

x 4 А

¨ -1 А

¨ -4 А

¨ 1 А

Задание {{98}}

Для представленной цепи собственное сопротивление третьего контура R₃₃ вычисляется по формуле

¨ -R₂-R₅-R₆

¨ R₁+ R₂- R₃

x R₂+ R₅ + R₆

¨ R₁+ R₂

Дата добавления: 2015-08-21