Закрите хешування

При закритому хешуванні в таблиці сегментів зберігаються безпосередньо елементи словника, а не заголовки списків. Тому в кожному сегменті може зберігатися тільки один елемент словника. При закритому хешуванні застосовується методика повторного хешування. Якщо ми спробуємо помістити елемент х в сегмент з номером h(x), який вже зайнятий іншим елементом (така ситуація називається колізією), то відповідно до методики повторного хешування вибирається послідовність інших номерів сегментів h1(x), h2(x), …, куди можна помістити елемент х. Кожне з цих місцеположень послідовно перевіряється, поки не буде знайдено вільне. Якщо вільних сегментів немає, то, отже, таблиця заповнена і елемент х вставити не можна.

Блок2

Купа, стіс або піраміда (англ. heap) в інформатиці — спеціалізована деревовидна структура даних, в якій існують певні властивості впорядкованості: якщо B — вузол B — тоді ключ(A) ≥ ключ(B). З цього випливає, що елемент з найбільшим ключем завжди є кореневим вузлом. Не існує ніяких обмежень щодо максимальної кількості елементів-нащадків повинна мати кожна ланка, однак, на практиці, за звичай, кожен елемент має не більше двох нащадків. Купа є однією із найефективніших реалізацій абстрактного типу даних, який має назву черга з пріоритетом. Купи відіграють критичну роль у низці ефективних алгоритмів роботи з графами, як то в алгоритмі Дейкстри та в алгоритмі сортуванняпірамідальне сортування. Найуживанішим класом куп є бінарні купи.

Базові операції з купою такі:

· підтримка основної властивості купи

· побудова купи з невпорядкованого масиву

· сортування купи

· видалення найменшого елемента

· отримання найбільшого елемента

· додавання елемента

Купи часто використовуються для моделювання черг з пріоритетами.

Блок2

Система (лес, объединение) непересекающихся множеств (СНМ, disjoint set forest, DSF, disjoint set union, DSU) – иерархическая структура данных, позволяющая эффективно работать с множествами. Рассмотри несколько упрощенную формулировку. Пусть у нас есть N занумерованных объектов (0, 1, … (N – 1)), причем каждый изначально находится в некотором одноэлементном множестве, то есть все объекты находятся в разных множествах.

ам требуется уметь эффективно выполнять 2 операции. Первая – объединить множество, содержащее x, с множеством, которое содержит y. Вторая – для данных x и y определить, принадлежат ли они одному множеству. Специфические, на первый взгляд, операции нужны, например, для алгоритма Краскала. Вообще, СНМ часто применяется в задачах на графы, так как позволяет эффективно работать с компонентами связности.

Поговорим о реализации. Каждое множество будет представляться деревом (их совокупность образует лес). Пусть номером множества, будет номер его корня. Так как все объекты имеют разные номера, а все множества не пересекаются, то номера всех множеств разные. Пусть для каждого элемента мы знаем ссылку на его предка в дереве. Для корня эта ссылка указывает на сам корень. Теперь мы можем легко определить номер множества в котором содержится элемент – идем по ссылке, пока она не зациклится в корне, номер которого мы и вернем. Чтобы ускорить работу, узнав номер множества, обновим все ссылки так, чтобы они сразу указывали на корень (это называется «сжатием путей»).

Объединение множеств выполняется очень просто: получаем номера множеств, если они совпали, то выходим. Иначе один корень «цепляем» к другому. В этом месте можно выполнить еще одну оптимизацию (так называемую «ранговую эвристику»). Для каждого множества будем хранить так называемый ранг. Он будет отражать высоту дерева (при сжатие путей он не будет пересчитываться, по этому реальной высотой его назвать нельзя). Теперь, когда мы объединяем два множества, то «цепляем» множество с меньшим рангом к множеству с большим рангом. Вообще можно отказаться от ранговой эвристики и делать объединение случайным образом, что тоже весьма эффективно. В любом случае, СНМ с указанными выше оптимизациями является оптимальной структурой для работы с непересекающимися множествами. Для разумных количеств объектов N и операций M можно полагать, что время работы будет O(M) (на самом деле оно несколько больше и равно O(M * a(N, M)), где a – обратная функция Аккермана).

Блок 1

Маши́на Тю́ринга — математичне поняття, введене для формального уточнення інтуїтивного поняття алгоритму. Названа на честь англійського математика Алана Тюринга, який запропонував це поняття у1936. Аналогічну конструкцію машини згодом і незалежно від Тюринга ввів американський математикЕміль Пост.

Основна ідея, що лежить в основі машини Тюринга, дуже проста. Машина Тюринга — це абстрактна машина (автомат), що працює зі стрічкою, що складається із окремих комірок, в яких записано символи. Машина також має голівку для запису та читання символів із комірок і яка може рухатись вздовж стрічки. На кожному кроці машина зчитує символ із комірки, на яку вказує голівка та, на основі зчитаного символу та внутрішнього стану, робиться наступний крок. При цьому, машина може змінити свій стан, записати інший символ в комірку або пересунути голівку на одну комірку ліворуч або праворуч

Формальні визначення алгоритму з'явилися в тридцятих-сорокових роках 20 століття. Одним із перших було визначення англійського математикаАлана Тюринга, який у 1936 році описав схему деякої гіпотетичної (абстрактної) машини і запропонував називати алгоритмами те, що вміє робити така машина. При цьому визначенні, якщо щось не може бути зроблено машиною Тюринга, це вже не алгоритм. Інакше кажучи, Тюринг формалізував правила виконання дій за допомогою опису роботи деякої конструкції.

У кожної машини Тюринга є стрічка, потенційно нескінченна в обидві сторони. Є скінченна множина символів стрічки S₀, …, S_n, що називається алфавітом машини. У кожен момент часу кожна комірка може бути зайнята не більш ніж одним символом. Машина має деяку скінченну множину внутрішніх станів q₀, q₁, …, q_n. У кожен даний момент часу машина знаходиться лише в одному із цих станів.

Нарешті, є голівка, яка у кожен даний момент часу знаходиться на одній із комірок стрічки. Машина діє не безупинно, а лише у дискретні моменти часу. Якщо у якийсь момент t голівка сприймає комірку (тобто знаходиться на комірці), що містить символ S_i, і машина знаходиться у внутрішньому стані q_j, то дія машини визначена однією із чотирьох дій:

1. голівка затирає символ S_i, і записує у тій же комірці новий символ S_k,

2. голівка пересувається в сусідню ліву комірку,

3. голівка пересувається в сусідню праву комірку,

4. машина зупиняється.

У випадках (1)-(3) машина переходить у новий внутрішній стан q_r, і готова знову до дії у наступний момент t + 1. Припустимо, що символ S₀ представляє порожню комірку, і отже, голівка завжди сприймає деякий символ.

Перші три з можливих дій машини можуть бути описані відповідно такими упорядкованими четвірками, які називаються командами:

1.

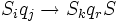
2.

3.

Тут перші два символа — це відповідно внутрішні стани машини і сприйнятий символ, наступні три визначають дію машини (запис голівкою символу S_k, або переміщення голівки на одну комірку вліво, або переміщення голівки на одну комірку вправо) та новий стан машини. Якщо стрічка вкладена в машину Тюринга, голівка машини встановлена на одну із комірок стрічки і машина приведена в один із своїх внутрішніх станів, то машина починає оперувати на стрічці: її голівка пише і стирає символи і пересувається з однієї комірки в іншу. Якщо при цьому машина колись зупиняється, то стрічка, яка розташована в ній в цей момент, називається результатом застосування машини до даної стрічки.

Незважаючи на свій простий устрій, машина Тюринга може виконувати складні перетворення слів. Спочатку, коли стрічка містить вхідне слово, автомат знаходиться проти деякої з комірок і у якомусь стані. У залежності від вибору початкової комірки, утворяться різні результати роботи машини Тюринга. У процесі своєї роботи машина Тюринга буде ніби перестрибувати з однієї комірки програми на іншу, відповідно до інформації на стрічці і вказівками в командах програми, поки не дійде до команди, яка переведе автомат у кінцевий стан.

Блок1

В інформатиці, недетермінований алгоритм це алгоритм, який передбачає декілька шляхів обробки одних і тих самих вхідних даних, без будь-якого уточнення який саме варіант буде обраний.

Часто в теорії алгоритмів, термін «algorithm» вказує на детермінований алгоритм. Недетермінований алгоритм відрізняється від свого відомішого двійника можливістю отримання результату декількома різними шляхами. Детермінований алгоритм передбачає єдиний шлях від вхідних даних до виходу, тоді як деякі шляхи виконання недетермінованого алгоритму можуть привести до однакового результату, а деякі до особливих результатів. Ці властивості описано математично в «недетермінованій» моделі обчислень, відомій як недетермінований автомат.

В розробці алгоритмів, недетерміновані алгоритми часто використовуються, коли задача, що розв'язується за допомогою алгоритму за своєю суттю дозволяє багато виходів (або коли існує один вихід з багатьма шляхами через які він може бути знайдений, при чому всі шляхи однаково добрі). Важливо, що кожен вихід недермінованого алгоритму правильний, незалежно від шляхів обраних алгоритмом під час виконання.

В теорії складності обчислень, недетермінований алгоритм є таким, що на кожному можливому кроці може бути декілька продовжень (уявіть людину, що простує лісом, кожного кроку вона повинна прийняти рішення, який шлях їй обрати далі). Такі алгоритми не видають розв'язок для кожного шляху обчислень; однак, вони гарантують отримання вірного розв'язку певним шляхом (наприклад, людина, що простує лісом може знайти свою хату, якщо обере певну комбінацію правильних шляхів). Вибори можна тлумачити припущення в процесі пошуку.

Велика кількість задач може бути осмислена через недетерміновані алгоритми, включно з найвідомішими нерозв'язаними питаннями в теорії обчислень, P = NP.

NP-повна задача (англ. NP-complete) — в теорії алгоритмів та теорії складності це задача, що належить докласу NP та всі задачі з класу NP можна звести до неї за поліноміальний час. Формальне означення:

Нехай — мова (проблема) що належить до класу NP. Мова називається NP-повною якщо виконуються такі умови:

1. належить до NP.

2. Для довільної мови в NP існує зведення до за поліноміальний час.^[2]

Якщо довільний окремий випадок задачі можна перетворити в деякий окремий випадок задачі в такий спосіб, що розв'язок задачі можна отримати за поліноміальний час від розв'язку задачі то кажуть, що зводиться до .^[1]

Якщо P ≠ NP, то всі NP-повні проблеми знаходяться в множині NP — P, через це доведення NP-повноти задачі можна розглядати як додатковий аргумент на користь того, що проблема не належить до класу P і для неї не існує точного поліноміального алгоритму.

Рівність класів P і NP вже більше 30 років є відкритою проблемою. Наукове співтовариство схиляється до негативного вирішення цього питання — у цьому випадку за поліноміальний час вирішувати NP-повні задачі не вдасться.

Дата добавления: 2015-08-21