Метод узловых потенциалов

МЕТОД КОНТУРНЫХ ТОКОВ

Перейдем к комплексной форме записи:

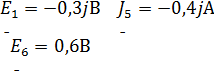
Пользуясь схемой на рисунке 2, составим систему уравнений контурных токов (1)[1].

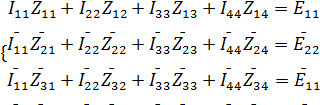
(1)

Контурный ток в четвёртом контуре вызывается лишь источником тока 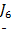, тогда

.

Перенесем свободные члены в системе (1) за знак равенства и, расписав суммы сопротивлений 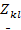и суммы ЭДС 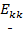, получим систему (2).

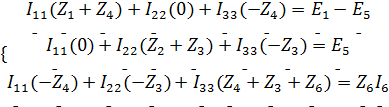
(2)

Подставим известные значения в систему (2), получим систему (3).

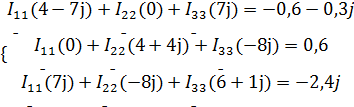
(3)

Решеим систему (3) с помощью программного пакета Mathlab[2], выполнив программу:

e1=-0.3j

e5=0.6

i6=-0.4j

z1=4

z2=4-4j

z3=8j

z4=-7j

z6=6

A=[z1+z4 0 -z4

0 z2+z3 -z3

-z4 -z3 z4+z3+z6]

B=[e1-e5

e5

i6*z6]

X=A\B

Теперь можно найти все контурные токи:

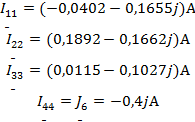
Из схемы (рисунок 2) видно как воздействую контурные токи на токи ветвей:

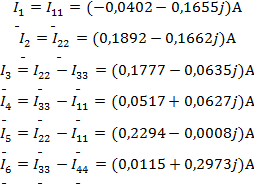
МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ

Пользуясь методом узловых потенциалов[1], по схеме, изображенной на рисунке 3, составим систему уравнений 4

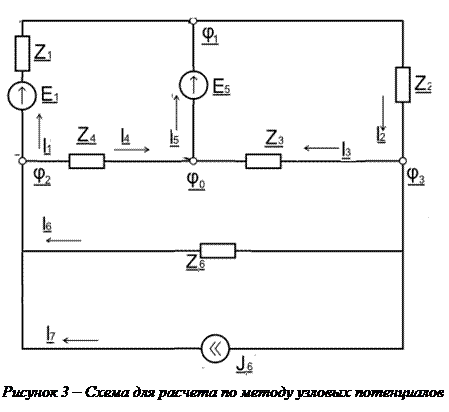
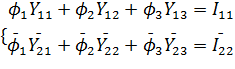
(4)

Так как 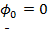, то 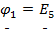. Перенесем в системе (4) свободные члены за знак равенства и, расписав суммы проводимостей и токов 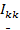, получим систему (5).

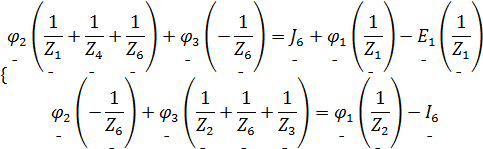
(5)

Подставив в систему (5) известные значения, получим систему (6).

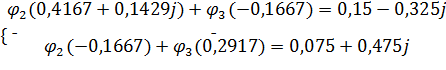
(6)

Решенив систему (6) получим значение потенциалов:

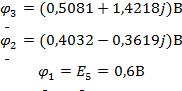
Теперь, используя закон Ома и первый закон Киргоффа, найдём токи в ветвях:

Дата добавления: 2015-08-21