Механика 1: Пространство

Любая игра имеет место в неком пространстве. Это пространство представляет собой “волшебный круг” геймплея. Оно определяет различные места, в которых существует игра, и то, как эти места соотносятся друг с другом. Являясь игровой механикой, пространство – это еще и математическая конструкция. Нам нужно отбросить все визуальное, всю эстетику, и просто посмотреть на абстрактную конструкцию игрового пространства.

Четко определенных правил описания этих абстрактных, упрощенных игровых пространств не существует. Хотя, принято считать, что игровые пространства:

1 Могут быть либо раздельными, либо бесконечными.

2 Имеют определенную размерность.

3 Состоят из ограниченных локаций, которые могут и не могут быть соединены.

Например, в игре крестики-нолики у нас есть раздельное и двухмерное поле. Что значит “раздельное”? Даже не понимая, что имеется в виду, мы рисуем поле для крестиков-ноликов, как вот это:

Рис. 10.1

Это определенно не бесконечное пространство, потому что нас интересуют только границы, а не пространство внутри каждой клетки. Куда бы мы ни поставили Х…

Рис. 10.2

Это не имеет значения – в рамках игры все эти положения эквивалентны. Но если поставить Х сюда:

Рис. 10.3

Это совсем другой случай. Даже несмотря на то, что игроки могут ставить свои отметки в бесконечном количестве мест и в бесконечном двумерном пространстве, существует всего девять разделенных точек, которые имеют значение в игре. В известном смысле, у нас есть девять нульмерных клеток, соединенных между собой двумерной решеткой, как на рисунке ниже:

Рис. 10.4

Каждый круг представляет собой нульмерное место, а каждая линия показывает, какие места соединены между собой. В крестиках-ноликах нет движения от места к месту, но смежность здесь очень важна. Без смежности это были бы просто девять разъединенных точек. Благодаря смежности мы имеем раздельное двумерное пространством с четко определенными границами – пространство в три клетки длиной и в три клетки шириной. То же самое можно сказать и о пространстве шахматной доски, лишь с тем исключением, что это пространство 8 х 8 клеток.

Вычурная эстетика игры может заставить вас подумать, что ее функциональное пространство более сложное, чем оно есть на самом деле. Давайте рассмотрим поле для Монополии.

С первого взгляда можно подумать, что это разделенное двухмерное пространство, похожее на шахматную доску, с которой убрали большинство центральных клеток. Но ее можно легко представить в виде одномерного пространства – линия из сорока разделенных точек, которые соединены между собой в виде замкнутой петли. Конечно, на игровом поле угловые пространства выглядят по-особенному, потому что они больше остальных, но функционально это не имеет значения, поскольку каждая игровая клетка представляет собой нульмерное пространство. Несколько игровых фишек могут стоять на одной клетке, но их взаимное положение внутри этой клетки не имеет функционального значения.

Но не все пространства раздельные. Стол для игры в пул может служить примером бесконечного двумерного пространства. Стол имеет закрепленную длину и ширину, а шар может свободно по нему перемещаться, отбиваясь от стенок или падая в лузы, которые тоже находятся в закрепленных местах. Никто не будет спорить с тем, что пространство бесконечное, но является ли оно двухмерным? Поскольку опытный игрок может заставлять шары вылетать за пределы стола и перепрыгивать друг через друга, можно говорить о том, что пространство игры на самом деле трехмерное, и в некоторых случаях подобные рассуждения могут быть полезными. Четко определенных правил для определения этих функциональных пространств не существует. Когда вы создаете новую игру, иногда полезно посмотреть на ее пространство как на двухмерное, но иногда представление этого пространства как трехмерного может быть более полезным. То же самое можно сказать о раздельном и бесконечном. Мы упрощаем игру до набора функциональных пространств для того, чтобы эстетика или реальный мир не мешали нам сосредоточиться на ней. Если вы думаете над тем, как можно изменить футбол, изменив границы игрового поля, вы, скорее всего, думаете об этом в рамках двухмерного бесконечного пространства.

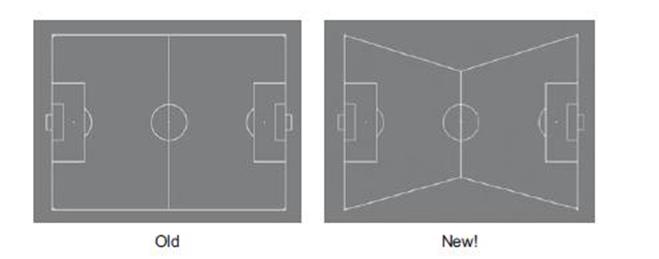
Рис. 10.5

Но если вы думаете об изменении высоты ворот, об изменении правил и о том, как высоко игрок может запустить мяч, или о добавлении на поле холмов и впадин, будет полезным рассмотреть это уже как бесконечное трехмерное пространство.

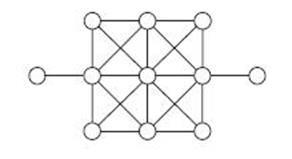
Рис. 10.6

Но, возможно, вы будете думать о футбольном поле как о раздельном пространстве – разделите его на, скажем, девять основных игровых зон и две дополнительные зоны справа и слева, которые будут вашими воротами. Этот способ мышления может вам пригодиться, когда вам, например, нужно будет проанализировать разные игровые типы на разных участках поля. Важно то, что вы сможете увидеть абстрактные модели вашего игрового пространства, что, в свою очередь, поможет вам лучше понять взаимосвязи вашей игры.

Дата добавления: 2015-09-03