Третье практическое занятие

В тех случаях, когда работы в режиме прямых вычислений для пользователя

недостаточно, MATLAB предусматривает возможность:

а) задать необходимые последовательности вычислений в виде

s c r i p t - ф а й л о в (или m-файлов) - аналогов внешних

процедур в языках высокого уровня,

б) создавать так называемые ф у н к ц и и п о л ь з о в а -

т е л я - m-файлы с описанием функций, которые после записи

на диск становятся для пользователя такими же доступными, как

встроенные функции sin, cos и т.д.

Такие конструкции создаются с помощью текстового редактора (File->New).

< ENTER >

П р и м е р 11. Создание script-файла.

Средствами редактора создадим файл с именем, например, model.m

(расширение.m при сохранении файла обязательно), содержащий

следующий текст:

x=1:0.1:10;

y=x.*sin(x)+2*cos(x);

plot(x,y);grid

< ENTER >

После записи файла model.m на диск и запуска системы MATLAB обратимся к нему

(в режиме прямых вычислений):

>> model

При этом будет выполнена последовательность команд, записанная в model.m, и

на экране появится график функции y(x)=x*sin(x)+2*cos(x) для аргументов x

из промежутка [1,10].

< ENTER >

Замечание.

Некоторые из базовых функций системы встроены в среду MATLAB, и их тексты

не доступны для пользователей. Остальные функции являются доступными и состав-

ляют библиотеку m-файлов,находящихся в поддиректориях

MATLAB\toolbox\matlab\datafun, MATLAB\toolbox\matlab\funfun.

Все m-файлы написаны в текстовом формате, и их можно просмотреть как внутри

системы, так и вне ее с помощью любого текстового редактора. Для начинающего

пользователя системы MATLAB при создании своих script-файлов эти m-файлы

рекомендуется использовать в качестве образцов.

<ENTER>

П р и м е р 12. Создание функции пользователя.

Пусть требуется задать функцию одной переменной х, зависящую от параметра а,

которая при x<a принимает значения y=a*x+1, а при x>=a - значения y=x^2+1.

Создадим с помощью редактора файл с именем func.m, содержащий следующий текст:

function y=func(x,a);

y=(x<a).*(a*x+1)+(x>=a).*(x.^2+1);

Функция func теперь стала функцией системы MATLAB, при запуске системы из той

директории, где записана func, пользователь может оперировать ею так же, как

и базовыми функциями системы (sin, cos, exp и т.п.). Например:

>> x=0:0.05:5;a=1.5;

>> y=func(x,a); % можно записать y=func(x,1.5)

>> plot(x,y);grid

Результатом выполнения этих действий является график функции func для значе-

ний х из промежутка [0,5].

< ENTER >

5. Основные правила программирования в системе MATLAB

*******************************************************

Входной язык системы MATLAB напоминает Бейсик (с элементами Фортрана

и Паскаля). Запись программ в системе традиционна, поэтому пользователь,

знакомый хотя бы с одним языком программирования высокого уровня, без тру-

да осваивает правила записи программ.

Главное правило требует постоянно помнить о том, что система MATLAB по

умолчанию предполагает, что каждая заданная переменная - это вектор или

матрица, и в соответствии с этим выполняет операции с переменными.

< ENTER >

5.1. Присваивание.

Операция присваивания задается знаком равенства:

ИМЯ ПЕРЕМЕННОЙ = ВЫРАЖЕНИЕ

Имя переменной может содержать до 31 символа и не должно совпадать с именами

функций и процедур системы. Переменные могут быть обычными и индексированны-

ми, а также текстовыми. Например,

>> х=5 % переменной х присвоено значение 5

>> v=[0 1 2 3] % задан вектор с элементами 0,1,2,3

>> txt='модель' % переменной txt присвоено символьное значение "модель"

5.2. Управляющие операторы

Язык системы MATLAB имеет управляющие структуры следующих типов:

if... end или if... else... elseif... end,

for... end,

while... end.

Например, вычисление факториала целого аргумента n(n!=1*2*...*n) можно орга-

низовать с помощью условного оператора и оператора цикла так:

>> n=23; nf=1; %вычисление 23!

>> if n>0 for i=1:n,

nf=nf*i; end;

end

Следует избегать циклов там, где MATLAB допускает альтернативные опера-

ции с векторами или матрицами (см. функции sum, cumsum, prod, cumprod,

find, size, max, min, sort и т.д.). Так вычислениe факториала n! правиль-

нее осуществить по-другому (это и проще и вычисляется быстрее):

>> n=23; % задание значения n

>> nf=prod(1:n) % вычисление произведения элементов вектора 1:n

< ENTE

% Пример создания script-файла.

x=1:0.1:10;

y=x.*sin(x)+2*cos(x);

plot(x,y);grid

% Создание script-файла. Пример 1

x=1:0.1:10;

y=x.*sin(x)+2*cos(x);

plot(x,y);grid

% Создание script-файла. Пример 2

a = input('Задайте первый коэффициент: a = ');

b = input('Задайте второй коэффициент: b = ');

x=0:0.01*pi:2*pi;

u=sin(a*x);

v=cos(b*x);

plot(u,v);grid

axis('square')

set(gca,'FontName','Courier')

title('ГРАФИК ФУНКЦИИ')

З а д а н и е

1. Проанализируйте текст m-файла primer1 и получите предусмотренный

этим файлом результат.

2. Проанализируйте текст m-файла primer2 и получите предусмотренный

этим файлом результат.

3. Познакомьтесь с традиционным оформлением текста m-функции в систе-

ме MATLAB на примере функции mean, вычисляющей среднее значение

(математическое ожидание). Для вывода на экран текста функции вос-

пользуйтесь оператором type.

4. Создайте свою функцию пользователя (см. пример 12), вычисляющую

значения заданной Вами функции одной переменной, зависящей от

одного параметра.

5. Создать script-файл, результатом выполнения которого является по-

строение графиков Вашей функции для трех значений параметра.

< ENTER >

Варианты заданий (m-функция)

N	f(x)	[ a, b ]
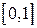
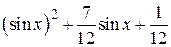
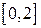
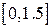
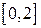
7.		[5,25]
		[0.1,10]
		[0.1,2]
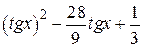
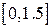
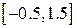
		[0,3]
		[0,2]
		[0,3]

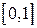
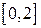
Дата добавления: 2015-09-03