Метод Монте-Карло (метод статистических испытаний)

Суть метода Монте-Карло (метода статистических испытаний) заключается в следующем. Для решения вычислительной задачи подбирается соответствующая вероятностная модель, в которую входит искомая неизвестная величина. Проводятся статистические испытания данной вероятностной модели с последующей статистической обработкой результатов ее многократных «наблюдений». В итоге получают оценку искомой величины. Иными словами моделируются входные случайные последовательности с заданными законами распределения. Каждый элемент входной последовательности преобразуется по алгоритму, соответствующему поставленной задаче. Полученная в итоге преобразований выходная случайная последовательность подвергается статистической обработке для определения той вероятностной характеристики, которая принимается за оценку искомой величины. Чаще всего такой вероятностной характеристикой является математическое ожидание.

Пусть требуется вычислить определенный интеграл . Если известно, что данная подынтегральная функция f(x) на интервале интегрирования 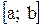не превышает некоторого значения С, то кривая располагается внутри прямоугольника с основанием (b − a) и высотой С (рис. 7.6).

Моделируют процесс случайного попадания точек в обозначенный прямоугольник. Для этого генерируют N пар случайных чисел и равномерно распределенных на интервалах 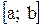и 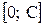соответственно. Каждая пара представляет собой координаты текущей точки. Таким образом получают N точек, равномерно рассеянных внутри прямоугольника.

Тогда приближенное значение интеграла (оценка интеграла) может быть вычислено по формуле:

(7.16)

где − количество точек, попавших под кривую N − общее количество точек (число испытаний, объем выборки); 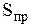− площадь прямоугольника.

Выражение тем точнее определяет значение интеграла , чем больше объем выборки N (общее количество точек), т. е.

(7.17)

Наиболее эффективен метод Монте-Карло при оценивании многомерных (кратных) интегралов. В отличие от других методов численного интегрирования трудоемкость метода Монте-Карло (объем вычислений) незначительно зависит от размерности решаемой задачи.

материальная

Дата добавления: 2015-09-03