Дэн Гилберт в знаменитой статье Вера и системы мышления показал, что мы отнюдь не рождаемся скептиками и что не верить — серьезное для нас умственное усилие. 4 страница

\384\

ЗОЛОТАЯ ПОСРЕДСТВЕННОСТЬ

Концепция Кетле пришлась весьма кстати идеологам того времени, которые как раз жаждали чего-либо подобного. Вы только взгляните на список его современников: Сен-Симон (1760-1825), Пьер-Жозеф Прудон (1809-1865), Карл Маркс (1818-1883), каждый — создатель своей версии социализма. В эпоху, последовавшую за веком Просвещения, все искали aurea mediocritas, золотую середину: в богатстве, росте, весе и т. д. Это стремление подчас заставляет принимать желаемое за действительное, оно во многом навеяно поисками гармонии и. платонизмом.

Я навсегда запомнил директиву своего отца — "in medio stat virtus", "доблесть — в умеренности". Да, долгое время это было идеалом; посредственность в этом смысле даже считалась золотой. Всеохватывающая посредственность.

Но Кетле поднял эту идею на новый уровень. На основе собранных им данных он начал создавать среднестатистические стандарты. Обхват груди, рост, вес детей при рождении — мало что избежало стандартизации. Отклонения от нормы, как он заметил, становятся экспоненциально более редкими с увеличением амплитуды отклонения. Покончив с физическими характеристиками, месье Кетле переключился на социальную сферу. L'homme moyen имел свои привычки, свои запросы, сбои методы.

Сконструировав таким образом Thornine moyen physique и 1'homme moyen moral (физического среднего человека и нравственного среднего человека), Кетле обозначил некие пределы отклонения от среднего, внутри которых любого человека помещают слева или справа от центра и, по сути, "бракуют" тех, кто оказывается у самого края. Их объявляют аномалией. Это, естественно, очень вдохновило Маркса, ко-

\385\

торыи ссылается на понятие среднего, или нормального, идивидуума, введенное Кетле. Он утверждает в "Капитале", что общественные различия (например, те, что обусловлены распределением капитала) должны быть сведены к минимуму.

Надо отдать должное научной элите времен Кетле. Коллеги настороженно отнеслись к его теории. Начнем с того, что Огюстен Курно, философ, математик, экономист, усомнился в том, что можно учредить некий стандарт человека только на основании количественных характеристик. Этот стандарт будет зависеть от рассматриваемой выборки. Замеры, произведенные в одной провинции, могут отличаться от замеров в другой провинции. Ну и какие из них должны быть эталоном? По мнению Курно, 1'homme moyen был бы чудовищем.

Я так поясню его мысль.

Даже если кому-то вдруг очень захотелось бы стать средним человеком, то ему пришлось бы утаить от "замерщиков" свои профессиональные таланты, то, в чем он неизбежно превосходит остальных, — человек не может быть средним во всем. Пианист будет лучше "среднего" играть на пианино, но хуже, чем предписано "нормой", ездить верхом. Чертежник будет лучше чертить и так далее. Понятие человека, считающегося средним, отличается от понятия человека, среднего во всем, что он делает. В действительности абсолютно средний человек был бы наполовину мужчиной, наполовину женщиной. Кетле совершенно упустил это из виду.

ошибка бога

Еще больше удручает то, что во времена Кетле гауссово распределение называлось "la loi des erreurs" — "закон погреш-

\386\

костей", так как одним из самых ранних его приложений было распределение погрешностей в астрономических расчетах. Вам тоже не по себе? С отклонением от среднего (в данном случае и от медианы тоже) обращались как с погрешностью! Не удивительно, что Марксу понравились идеи Кетле.

Понятие усредненности распространилось мгновенно. "Так положено" спутали с "есть" — и все это с благословения науки. Понятие середняка глубоко вошло в культуру, ожидавшую нарождения европейского среднего класса, в молодую культуру постнаполеоновского лавочника, опасающегося излишнего богатства и интеллектуального блеска. В принципе считается, что мечта об обществе с нивелированными доходами отвечает стремлениям всякого рационально мыслящего человека, вынужденного иметь дело с генетической лотереей. Если бы вам предложили выбрать общество, в котором вы родитесь в следующей жизни, но неизвестно кем именно, скорее всего вы не стали бы рисковать — предпочли бы такое общество, в котором нет существенной разницы в доходах.

Курьезной кульминацией восхваления посредственности стало появление во Франции так называемого "пужадизма"*, политического движения, начавшегося с выступлений лавочников. Это было горячее братство людей более или менее благополучных, надеявшихся, что вся остальная вселенная подстроится под них — своего рода случай непролетарской революции. Их мелкоторгашеский менталитет проявлялся даже в том, как они обращались с математикой. Думал ли Гаусс, что создает формулы для лавочников?

* Термин "пужадизм" образован от имени Пьера Пужада (1920-2003)- В1553 г. он основал крайне правый "Союз по зашите владельцев магазинов и ремесленников", а в 1956 г. —-политическую партию "Союз французского братства", получившую свыше и% голосов избирателей на последних парламентских выборах Четвертой республики, (Лрои. ред.')

\387\

ПУАНКАРЕ ПРИХОДИТ НА ПОМОЩЬ

Сам Пуанкаре относился к гауссиане с большой опаской. Я подозреваю, что он внутренне съеживался, когда ему предлагали этот и подобные подходы к моделированию неопределенности. Достаточно вспомнить, что колоколовидная кривая изначально предназначалась для измерения астрономических погрешностей, а уже небесная механика самого Пуанкаре проникнута куда более глубоким пониманием неопределенности.

Пуанкаре писал, что один из его друзей, "выдающийся физик", жаловался ему, что физики пользуются "гауссовой кривой", потому что, вслед за математиками, считают ее математической необходимостью, математики же пользуются ею, потому что считают ее эмпирической данностью.

будем справедливы

Хочу особо отметить, что вообще-то (если оставить в стороне издержки в виде психологии лавочников) я искренне верю в ценность срединности и посредственности — какой гуманист не мечтает уменьшить неравенство между людьми? Нет ничего более отталкивающего, чем безрассудно сотворенный идеал сверхчеловека! На самом деле меня тревожит Иная проблема — эпистемологическая, то есть проблема познания. Пора уяснить, что реальность — не Среднестан и нам Надо научиться с этим жить.

"греки бы его обожествили"

Список людей, у которых в мозгу угнездилась [благодаря своей платонической чистоте) гауссиана, невероятно велик.

\388\

Сэр Фрэнсис Гальтон, двоюродный брат Чарльза Дарвина и внук Эразма Дарвина, был наряду со своим кузеном одним из последних независимых ученых-джентльменов, к каковым также принадлежали лорд Кавендиш, лорд Кельвин, Людвиг Витгенштейн (на свой лад) и отчасти наш суперфилософ Бертран Рассел. Хотя Джон Мэйнард Кейнс не вполне вписывался в эту категорию, он мыслил в унисон с ней. Гальтон жил в викторианскую эпоху, когда обладатели наследственного состояния и неограниченного досуга не только упражнялись в верховой езде и стрельбе по дичи, но становились философами, учеными или (менее одаренные) политиками. Как это ни печально, вместе с той эпохой ушло нечто невосполнимое: истинные подвижники, занимающиеся наукой ради науки, не думающие о карьере.

К сожалению, занятия наукой из бескорыстной любви к знанию не гарантируют, что ты будешь двигаться в правильном направлении. Познакомившись с "нормальным" распределением, Гальтон влюбился в него. Говорят, он однажды воскликнул, что, если бы грекам было о нем известно, они бы обожествили его. Возможно, восторг Гальтона тоже поспособствовал воцарению гауссианы в научных умах.

Гальтон не сподобился обзавестись надлежащим математическим багажом, но был прямо-таки одержим измерениями. Он не знал о законе больших чисел, но сам открыл его, проанализировав собранные данные. Он сконструировал

доску Гальтона, или "quincunx"

что-то вроде автомата

для игры в пинбол, с помощью которого можно смоделировать колоколовидную кривую, — об этом я расскажу через несколько абзацев. Правда, Гальтон применял кривую нормального распределения в таких областях, как генетика и на-

* Шахматный порядок (лат.).

\389\

следственность, где ее использование оправданно. Но его энтузиазм помог внедрить зарождавшиеся статистические методы в социальные сферы.

ответьте, пожалуйста, "да" или "нет"

А сейчас позвольте мне поговорить о размерах ущерба.

Если вам нужны качественные (а не количественные) выводы, как в психологии или медицине, где вы вполне обойдетесь "безразмерными" ответами "да" или "нет", то можете спокойно допустить, что находитесь в Среднестане. Влияние невероятного не будет слишком большим. У него есть рак либо нет; она беременна либо нет и так далее. Смертельность или беременность не имеют степеней (если не рассматривать их в эпидемических масштабах). Но, когда вы манипулируете совокупностями, различными по величине (такими как доход, ваш капитал, прибыль с портфеля ценных бумаг или продажи книг), гауссиана может вас здорово подвести, так как эта сфера не в ее компетенции. Одно-единственное число способно порушить все ваши средние показатели; одна-единственная потеря — зачеркнуть сотни и сотни прибылей. Уже нельзя говорить: "Это исключение". Заявление "да, я могу потерять деньги" довольно бессмысленно, если не указать хотя бы приблизительную сумму. Потерять весь свой капитал или потерять долю своего дневного дохода — все-таки разница.

Именно поэтому эмпирическая психология и открытые ею свойства человеческой природы, о которых я говорил в начале этой книги, не страдают от ложного использования гауссианы; психологам вообще повезло, ибо переменные, которыми они оперируют, в большинстве своем не выходят за рамки обычной гауссовой статистики. Выясняя, сколько

\390\

человек в выборке имеют определенную особенность или склонность к ошибке, они обычно добиваются результата посредством ответов "да" или "нет". Ни одно отдельно взятое наблюдение не может в корне изменить общего заключения. Теперь я представлю вам идею гауссианы, разобрав ее по кирпичикам.

МЫСЛЕННЫЙ СЧИСЛЕННЫЙ)

ЭКСПЕРИМЕНТ, ДЕМОНСТРИРУЮЩИЙ,

ОТКУДА ПРОИСХОДИТ КРИВАЯ

НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ

Рассмотрим своего рода пинбольный автомат, такой, как на рисунке 8. Запустим 32 шара, предполагая, что доска правильно сбалансирована, так что у шара одинаковые шансы свалиться направо и налево на любом пересечении, наткнувшись на штырь. Ожидаемый результат — большая часть шаров "приземлится" в центральных ячейках: чем ячейки дальше от центра, тем меньше туда попадет шаров.

Затем проведем мысленный эксперимент. Человек бросает монетку, смотрит, что выпало, орел или решка, и в зависимости от этого делает шаг влево или вправо. Это так называемое "случайное блуждание" не обязательно связано с ходьбой. С таким же успехом можно представить, что вместо шага вправо или влево вы каждый раз выигрываете или проигрываете доллар, при этом ведя учет долларам, накопившимся у вас в кармане.

Предположим, я заключаю с вами честное пари, где возможность выигрыша у вас примерно та же, что и проигрыша. Кидаем монетку. Орел — вы получаете доллар, решка — теряете доллар.

\391\

Рис. 8. Доска Гальтона, ил и "quincunx" (в упрощении), - автомат для игры в пинбол

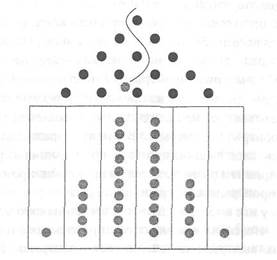
Падающие шары, ударяясь о штыри, произвольно скатываются то вправо, то влево. На рисунке — самый вероятный сценарий, который очень похож на кривую нормального (то есть гауссова] распределения. Любезное приношение А л ександр а Талеба.

При первом броске вы либо выиграете, либо проиграете.

При втором броске число возможных исходов удваивается. Вариант г. выигрыш-выигрыш. Вариант 2: выигрыш-проигрыш. Вариант з: проигрыш-выигрыш. Вариант 4' проигрыш-проигрыш. У каждого из этих вариантов одинаковые шансы, комбинация из одного выигрыша и одного проигрыша встречается вдвое чаще, так как варианты 2 и з, выигрыш-проигрыш и проигрыш-выигрыш, приводят к одинаковому результату. И в этом ключ к гауссиане. В середине очень многое сглаживается, и, как мы увидим, к середине тяготеет большинство. Поэтому если при каждом броске разыг-

\392\

рывается доллар, то на втором броске ваши шансы таковы: 25 процентов, что вы приобретете или потеряете 2 доллара, и 50 процентов, что выйдете в нуль.

Третий бросок снова удваивает число исходов, так что их становится восемь. Вариант i (выигрыш-выигрыш после двух бросков) разветвляется на выигрыш-выигрыш-выигрыш и выигрыш-выигрыш-проигрыш. Мы добавляем выигрыш или проигрыш к каждому из предыдущих результатов. Вариант 2 разветвляется на выигрыш-проигрыш-выигрыш и выигрыш-проигрыш-проигрыш. Вариант з разветвляется на проигрыш- выигрыш-выигрыш и проигрыш-выигрыш-проигрыш. Вариант 4 разветвляется на проигрыш-проигрыш-выигрыш и проигрыш-проигрыш-проигрыш.

Теперь у нас восемь вариантов., все одинаково вероятные. Заметим, что снова можно сгруппировать средние исходы, в которых выигрыш перечеркивает проигрыш. (На доске Гальтона ситуации, когда шар отлетает влево, а затем вправо, или наоборот, преобладают, так что в результате в середине оказывается много шаров.)

Совокупный итог таков: i) три выигрыша; 2) два выигрыша, один проигрыш, итого один выигрыш; з) два выигрыша, один проигрыш, итого один выигрыш; 4) один выигрыш, два проигрыша, итого один проигрыш; 5) два выигрыша, один проигрыш, итого один выигрыш; 6) два проигрыша, один выигрыш, итого один проигрыш; у) два проигрыша, один выигрыш, итого один проигрыш; и, наконец, 8) три проигрыша.

Из восьми вариантов вариант трех выигрышей встречается однажды. Вариант трех проигрышей встречается однажды. Вариант одного итогового проигрыша (один выигрыш, два проигрыша) встречается три раза. Вариант одного итогового выигрыша (один проигрыш, два выигрыша) встречается три раза.

\393\

Сделаем еще один бросок, четвертый. Будет шестнадцать равновероятных исходов. Один вариант четырех выигрышей, один вариант четырех проигрышей, четыре варианта двух выигрышей, четыре варианта двух проигрышей и шесть вариантов выхода в нуль.

"Quincunx" (это латинское производное от числительного "пять") в нашем пинбольном примере представляет собой иллюстрацию пятого броска или шага, после которого шансы, как легко высчитать, возрастают до шестидесяти четырех. Вот идея, воплощенная в доске Фрэнсиса Гальтона. Гальтону явно недоставало здоровой лени и математической сметки: вместо того чтобы сооружать такое устройство, вообще-то проще было поработать с алгеброй или провести мысленный эксперимент вроде нашего.

Однако продолжим игру до сорокового броска. На это уйдет лишь несколько минут, но понадобится калькулятор, чтобы вычислить количество исходов, так как наши мозги с этим не справятся. Получится i 099 5¹¹ 627 776 возможных комбинаций — то есть более тысячи миллиардов. Не затрудняйтесь просчитывать шаг за шагом — это будет два в сороковой степени, так как на каждом этапе каждая цепочка раздваивается. (Вспомните, как мы добавили выигрыш и проигрыш к вариантам третьего броска, удвоив число вариантов.) Из этих комбинаций только одна будет состоять из сорока выигрышей и только одна — из сорока проигрышей. Остальные будут тяготеть к середине, в данном случае — к нулю.

Вам уже ясно, что этот тип случайности чрезвычайно беден крайностями. Все сорок бросков оказываются выигрышными лишь в одном случае из i 099 5U 627 7?б. Если вы станете час за часом проделывать это упражнение с сорока бросками, вам придется здорово попотеть, прежде

\394\

чем выпадут сорок орлов (или сорок решек) подряд. Поскольку вы наверняка будете прерываться, чтобы поесть, поспорить с друзьями и соседями, попить пива и поспать, то готовьтесь, ради такой удачи, прожить около четырех миллионов жизней. А представьте, что вы добавляете один лишний бросок. Чтобы выкинуть орла сорок один раз подряд, понадобится потратить на попытки восемь миллионов жизней! Переход от 4° к 41 уменьшает шансы вдвое. Это — ключевое свойство немасштабируемого подхода к анализу случайности: крайние отклонения убывают с все возрастающей скоростью. А пятьдесят орлов подряд могут выпасть один-единственный раз на протяжении 4 миллиардов жизней!

Мы еще не получили "гауссову кривую", но сильно приблизились к ней. Пока это протогауссиана, но суть уже видна. (На самом деле вы никогда не встретите "гауссову кривую" в чистом виде, так как это платоническая фигура — к ней можно только стремиться, но достичь ее невозможно.) Но, как показывает рисунок д, знакомая колоколовидная форма уже просматривается.

Способны ли мы ближе подойти к совершенной "гауссовой кривой"? Да. Для этого нужно разбить раунд на большее количество менее результативных бросков. Можно ставить на кон не доллар, а десять пенсов и бросать не 40, а 4000 раз, складывая результаты. Ожидаемый риск будет приблизительно тем же — и в этом фокус. В соотношении двух названных вариантов игры есть небольшой сознательный сдвиг. Мы умножили число бросков на юо, но поделили размер ставки на ю — не ищите сейчас причины, просто предположите, что варианты "эквивалентны". Общий риск эквивалентен, но теперь нам открылась возможность выиграть или проиграть 4° долларов за 400 последовательных

\395\

Рис. 9. Количество выигрышей и проигрышей

Результат сорока бросков. Протогауссиана отчетливо вырисовывается.

бросков. Шансы равны единице на единицу со 12о нулями, то есть i/i ооо ооо ооо ооо ооо ооо ооо ооо ооо ооо ооо

Дата добавления: 2015-09-03