Характеристика нагруженности машин в вероятностном аспекте

Нагруженность машин и отдельных деталей, подлежащих расчету на сопротивление усталости, характеризуют соответствующим спектром нагрузок, т. е. совокупностью значений, которые может принимать нагрузка. Спектры нагрузок могут быть дискретными или непрерывными.

Обычно дискретные спектры (рис. 4.2) представляют вкоординатах: нагрузка F – относительная продолжительность р действия нагрузки или в координатах суммарная продолжительность Σ р _i действия – нагрузки в порядке убывания (ранжированный спектр). Первая форма может рассматриваться как дифференциальная, вторая как интегральная.

Для непрерывного спектра нагрузок задают функцию плотности распределения f(F) (рис. 4.3, а) или интегральную функцию . Последняя физически означает долю продолжитель­ности действия нагрузки меньше данной величины или соответст­вующую вероятность, что нагрузка меньше данной величины.

Практически чаще пользуются интегральными графиками не­прерывных распределений (рис. 4.3, б) в координатах ранжирован­ного спектра, т. е. нагрузка откладывается по оси ординат, а соот­ветственно по оси абсцисс – функция 1– P(F), которая означает долю продолжительности действия нагрузки больше данной вели­чины или соответствующую вероятность.

Использование непрерывного плавного спектра в расчетах не всегда удобно, поэтому в целях упрощения функции f(F) и 1– P(F) могут быть заменены ступенчатыми кривыми (рис. 4.3). Для этого интервал возможных нагрузок разбивают на равномерные участки Δ F; среднее значение нагрузки i - го участка обозначают через F_i. Тогда относительная продолжительность действия нагрузки F_i рав­на p_i = f (F_i)Δ F.

Статистический анализ нагруженности машин различных типов показал, что при всем многообразии спектров нагрузок их можно свести к нескольким типовым. Это становится очевидным при пред­ставлении нагруженности в виде спектра относительных нагрузок, обычно выраженных в долях от максимальной.

Функции плотности f(F/F_max) и интегральные функции 1 – P(F/F_max) спектров относительных нагрузок для типовых режи­мов нагружений приведены на рис. 4.4. Для описания спектров нагрузок тяжелого (рис. 4.4, кривая 1), легкого (кривая 4)и особо легкого (кривая 5)режимов используются функции бета-распреде­ления; для среднего равновероятного режима (кривая 2)– функция равновероятного распределения; для среднего нормального (кри­вая 3)– функция нормального распределения.

В соответствии со структурой формул расчета на сопротивле­ние усталости при переменных амплитудах нагрузок, в частности при переменных режимах, спектры нагрузок удобно задавать их начальными моментами μ_k Индекс k =1, 2, 3... в обозначении соответствует порядку начального момента.

Начальные моменты k- гопорядка определяют по формулам: для дискретных спектров нагрузок

μ _k = Σ(F_i / F_max)^k ∙ p _i;

для непрерывных спектров нагрузок

.

Начальные моменты отражают основные свойства спектра: на­чальный момент первого порядка равен среднему значению и ха­рактеризует центр группирования нагрузок спектра; первый и второй начальные моменты — рассеяние (дисперсию) нагрузки от носительно центра группирования; первые три начальные момен­та — асимметрию распределения нагрузок и т. д.

В расчетах деталей машин на сопротивление усталости бази­руются на гипотезе линейного суммирования повреждений. При определении эквивалентного числа циклов перемен напряжений ис­пользуют коэффициент эквивалентности циклов k_EN, равный на­чальному моменту k- гопорядка μ _kт. е. k_EN = μ _kПри определе­нии эквивалентной нагрузки используют коэффициент эквивалент­ности режима нагружений К _реж, равный ^,где порядок начального момента совпадает с показателем степени k и выбира­ется в зависимости от показателя степени т кривой усталости в ко­ординатах напряжение — число циклов перемен напряжений. Так, при напряжениях, пропорциональных нагрузке, k = m. При кон­тактных напряжениях, пропорциональных корню квадратному из нагрузки, порядок начального момента k = m /2.

Значения начальных моментов k- гопорядка для спектров отно­сительных нагрузок типовых режимов нагружений приведены в табл. 4.1.

Для расчетов на прочность нагруженность может быть задана максимальной нагрузкой F_max и соответствующим начальным мо­ментом μ _k спектра относительных нагрузок. Учитывая случайный характер нагрузок, обе величины должны рассматриваться в ве­роятностном аспекте.

Таблица 4.1.

Режим	Порядок начального момента k
Тяжелый	0,772	0,615	0,501	0,300	0,200	0,142
Средний равновероятный	0,500	0,333	0,250	0,143	0,100	0,077
Средний нормальный	0,500	0,286	0,179	0,065	0,036	0,0266
Легкий	0,423	0,218	0,127	0,0384	0,0164	0,00845
Особо легкий	0,310	0,128	0,0622	0,0126	0,00408	0,00169

Линейное правило суммирования повреждений

При нестационарных нагрузках для оценки работоспособности деталей исполь­зуют представления об эквивалентных режимах и запасах прочности.

Предположим, что деталь работает в переменном режиме нагружения, имеющем k ступеней (рис. 3.4, о); i -номер ступени нагрузки, i = l, 2,..., k), и на каждой i -й ступени (точка A на рис. 3.4, б) испытывает N _i циклов нагружений. Обозначим через Ni, число циклов нагру­жений детали при работе на i -й ступени до разрушения (точка А,на кривой уста­лости, см. рис. 3.4, б).

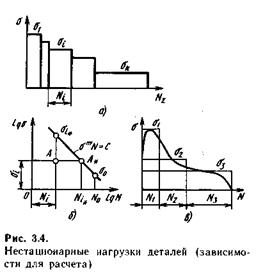Полагают, что разрушение детали при действии циклических постоянных напряжений (работа на одной ступени) через N. циклов нагружений происходит в результате постепенного накопления в материале повреждений (необратимых изменений в виде микротрещин и др.). Если через П обозначить меру повреждений, то в начальный момент работы детали П = 0, а в момент разрушения П = 1. Степень повреждений детали можно приближенно оценить относительной долговечностью

П_i= N_i / N_i*

Экспериментально установлено, что при работе на нескольких ступенях повреждения продолжают независимо нарастать пропорционально соответствующей относительной долговечности и потому могут линейно суммироваться (принцип линейного суммирования повреждений), т. е.

П = П ₁ + П ₂ + П ₃ + … + П _k = (3.9)

Условие разрушения имеет вид

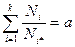. (3.10)

Если рассмотреть некоторый эквива­лентный стационарный (постоянный) ре­жим, на котором деталь приобретает ту же степень повреждения, и в качестве эквивалентного принять режим с напря­жением σ_экв= σ₀ и долговечностью N ₀, то из уравнения кривой усталости следует 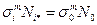, откуда

,

где σ₀ — предел выносливости детали на базе испытаний N₀ циклов.

Подставляя это равенство в условие разрушения (3.10), получим

(3.11)

Обычно принимают а = 1, N ₀ = 10⁷ циклов.

Соотношение (3.11) используют и для определения эквивалентной нагрузки F _экв (силы, вращающего момента), если заданы нагрузки на отдельных ступенях:

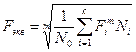, (3.12)

Если через п _i = σ_i* / σ_i (см. рис. 3.4, б) обозначить частный запас прочности или запас прочности на i -й ступени нагруже­ния, то из уравнения кривой усталости 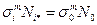следует .

Подставляя это соотношение в условие разрушения, получим

. (3.13)

Поставим нестационарному режиму в соответствие эквивалентный стационарный режим с запасом прочности п_жв, для кото­рого условие разрушения будет

1/ n _экв = а. (3.14)

Приравнивая соотношения (3.13) и (3.14), получим формулу для запаса прочности при ступенчатом нагружении

. (3.15)

Дата добавления: 2015-09-03