РЕШЕНИЕ. 1.Координаты точек естественной механической характеристики: первой [n=n0 и М=0]

1. Координаты точек естественной механической характеристики: первой [n=n₀ и М=0], второй [n = n_н и М = Мн].

Из соотношения:

находим

Номинальный вращающий момент двигателя:

В первом квадранте построим естественную механическую характеристику (рисунок 2, прямая 1).

2.Механическая характеристика в генераторном режиме (второй квадрант на рисунке 2, прямая 2) имеет координаты: первая точка [n =1070 об/мин. и М = 0], вторая точка [n₁= 1200 об/мин и М = - Мн = - 204 Нм].

Добавочное сопротивление R₁, которое необходимо включить в цепь якоря, чтобы получить такую механическую характеристику в генераторном режиме, найдем из уравнения электрического равновесия:

.

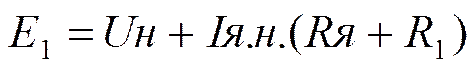Откуда:

(2)

Найдем Е₁ - э.д.с. двигателя в генераторном режиме из соотношения:

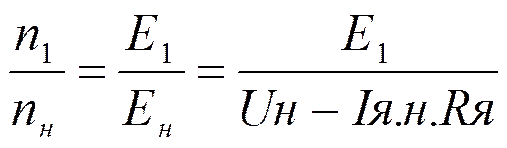
или

.

Тогда:

n,

об/мин

1200 –

2 nо

1000 - 1

nн

800 -

600 -

400 -

3

200 -

___________-Мн__________________________________________Мн______________

^{1 1 1 1 1 1 1 1 1 1}

-М,Нм -250 –200 -150 -100 -50 -- 50 100 150 200 250 М,Нм

-400 -

двигательный режим,

генераторный режим,

динамическое торможение

противовключения

Рис.2 Механические характеристики двигателя постоянного тока параллельного возбуждения в различных режимах работы

3.В режиме динамического торможения (второй квадрант) координаты точек механической характеристики следующие: первая [n=0 и М=0], вторая [n =n ₂=210об/мин и М=-Мн= - 204 Нм].

При этом добавочное сопротивление, которое необходимо включить в цепь якоря для того, чтобы получить механическую характеристику в динамическом режиме, находим из уравнения электрического равновесия, имея в виду то, что Uн = 0:

или

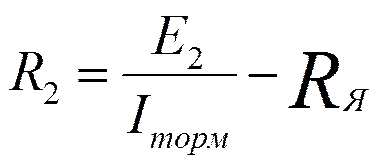(3)

Величину Е₂ в динамическом торможении находится из соотношения:

Откуда:

.

Тогда:

4.В режиме противовключения за счет тормозного спуска (четвертый квадрант на рисунке 2, прямая 4) координаты точек для построения механической характеристики следующие:

Первой [n = n₀ = 1070 об/мин. и М = 0]; второй [n = n₃ = - 210 об/мин. и М = Мн = 204 Нм].

Добавочное сопротивление R₃, которое необходимо включить в цепь якоря двигателя, чтобы получить механическую характеристику в режиме торможения противовключением при n₃ = - 210 об/мин., находят из уравнения равенства э.д.с. для этого режима:

откуда:

(4)

Величину Е₃ определяем из соотношения:

,

отсюда:

Так как n₂ = n₃ , то и Е₂ = Е₃ = 43,4 В.

Поэтому:

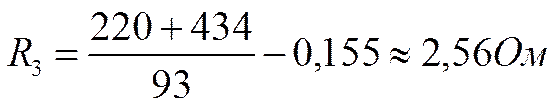
Аналитическое выражение механической характеристики для двигательного режима описывается уравнением вида:

(5)

где y = n, х = М, a = n_о = 1070 об/мин.

Для точки с номинальными параметрами уравнение (5) примет вид:

n_н = n_о +k*Мн

откуда:

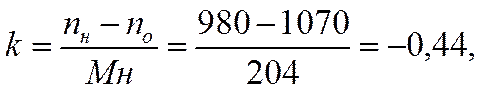
Следовательно, уравнение механической характеристики в двигательном режиме примет вид:

Аналитическое выражение механической характеристики для режима генераторного торможения (прямая 2) аналогично выражению для прямой 1.

Аналитическое выражение механической характеристики для режима динамического торможения (прямая 3) в общем виде описывается выражением:

У = - kх,

где у = n, х = М.

Для точки с номинальными параметрами: n_н = - k Мн, то есть

Следовательно, механическая характеристика динамического режима описывается уравнением вида:

n = - 4,8* М

Аналитическое выражение механической характеристики для режима противовключение(прямая 4) в общем виде описывается уравнением (5) и для точки с координатами n₃ = -210 об/мин. и М = Мн = 203Нм примет вид:

-n₃ = n_о + k*Мн,

откуда

.

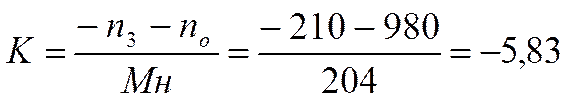Поэтому уравнение режима противовключения имеет вид:

n = n_о – 5,83*М

Дата добавления: 2015-09-03