Правила дифференцирования

Производная

Определения

Производной функции у = f(x) называется предел отношения приращения функции D у к приращению аргумента D х, когда D х стремится к нулю:

Рис. 2.

Геометрический смысл производной:

– тангенс угла наклона α касательной к графику функции у = f(x) в точке с абсциссой х₀ (рис. 2).

Физический смысл производной: S'(t) = v(t) – скорость движения тела в момент времени t при прохождении пути S(t).

Функция, имеющая производную, называется дифференцируемой. Операция нахождения производной называется дифференцированием.

Таблица производных

Название функции	Производная
Степенная x ^a
Натуральный логарифм ln x
Логарифмическая loga x, (a > 0, a ¹ 1)
Показательная a^x, (a > 0, a ¹ 1)
Экспоненциальная e^x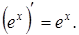
Тригонометрические
Синус sin x
Косинус cos x
Тангенс tg x илиtan x
Котангенс ctg x или cot x
Обратные тригонометрические
Арксинус arcsin x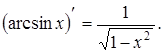
Арктангенс arctg x или atan x

Правила дифференцирования

1. Производная постоянной C равна нулю:

C ' = 0.

2. Производная суммы двух функций равна сумме производных этих функций:

(u(x) + v(x))' = u'(x) + v'(x).

3. Производная произведения двух функций:

(и(x)∙v(x))' = и'(x)∙v(x)+ v'(x)∙и(x).

В частности, (Си(x))' = Си'(x).

4. Производная частного двух функций:

5. Производная сложной функции: если

у = f(u), и = и(х),

то

то есть производная сложной функции по независимой переменной x равна произведению производной этой функции по промежуточной переменной и на производную промежуточной переменной по независимой переменной х.

6. Производная обратной функции.

Если y = f(x) – монотонная непрерывная функция, то она имеет обратную функцию x = g (у) у = f (g (y)) и x = g(f(x)), и их производные связаны равенством

.

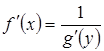Пример 7. Найти производную функции

Решение. Применим формулы для производной произведения двух функций и производной сложной функции для каждой из них.

Для :

,

аналогично для w (x). В итоге:

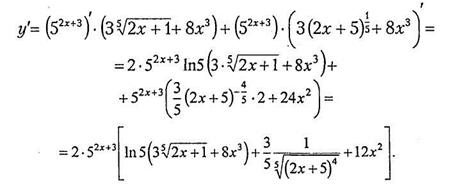
Пример 8. Найти производную функции y = tg⁵(4 x ³+7cos2 x).

Решение. Применим формулу для производной сложной функции:

Пример 9. Найти производную функции

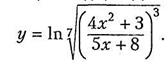
Решение. Сначала преобразуем исходную функцию, используя свойства логарифма:

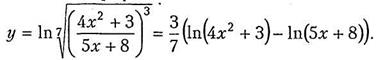
Найдём производную:

Дата добавления: 2015-10-23