Модуль 3.8.1. Методичні вказівки. Варіант 0.

Задача 1. Кидають 3 гральні кубика. Знайти ймовірність того, що на верхніх гранях випадуть числа очок, які всі є однаковими.

Нехай, подія А – всі числа однакові.

n = 6*6*6=6³ кількість варіантів випадання чисел на 3-х кубиках.

m =6 – кількість варіантів випадання чисел очки, яких є всі однаковими (111, 222, 333, 444, 555, 666)

Р =

Р(А) = =

Задача 2. Слово складено з карток, на кожній з котрих написано 1 літеру. Потім картки змішують і виймають по 1 без повторення. Знайти ймовірність того, що в результаті викладання в порядку їх появи утвориться наступне слово “ректор”.

Подія А – утвориться слово “ректор”

Р =

Р(А) = =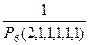

Задача 3. Нехай ваше прізвище та ім’я записано за допомогою карток. Картки з буквами прізвища і імені змішують в окремі стоси і окремо виймають навмання по 1 картці без повторення. Знайти ймовірність того, що букви, які викладають по черзі утворять ваше прізвище та ім’я.

Шептилевська Катерина.

Подія А – складається прізвище та ім’я.

Подія В - складається прізвище

Подія С - складається ім’я

Р(А) = Р(В) х Р(С)

Подія В: n = 12!; m = 2!

P(B) = = = =

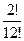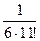
Подія С: n = 8!; m = 2!

P(C) = = = =

P(A) = =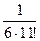

Задача 4. В урні міститься К чорних і Н білих куль. Навмання виймають М куль. Знайти ймовірність того, що серед них є:

1. Р білих куль;

2. Менше ніж Р білих куль;

3. Хоча б одна біла куля.

К = 6; Н = 7; М = 5; Р = 2

(6 чорних, 7 білих, виймають 5)

1) А - серед п’яти вибраних куль 2 білих, отже і 3 чорних.

n = C₁₃⁵ = = = = 13 11 9

m = C₇² C₆³ = = = 21 20

P(A) = = = 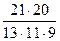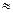0,326

2) В - вийняли менше 2-х білих куль.

n= C₁₃⁵ = 13 11 9; m = C₇¹ C₆⁴ + C₇⁰ C₆⁵ = + 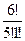= 7 15 + 6 = 111

P(B) = = = 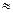0,086

3) С – хоча б одна біла куля.

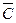- жодної білої кулі

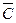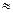P(C) = 1 – P() = 1 - = 1 - = 1 - = 0.995

Задача 5. Прилад складається з трьох незалежних елементів, які працюють на протязі часу Т безвідмовно із ймовірністями р,р,р. Знайти імовірність того, що за час Т вийде з ладу:

1) тільки один елемент;

2) хоча б один елемент.

к = 0,131

р₁ = 0,869 q₁ = 0,131

р₂ = 0,769 q₂ = 0,231

р₃ = 0,719 q₃ = 0,281

р_і – імовірність того, що відповідний елемент не вийде з ладу.

q_I - імовірність того, що елемент вийде з ладу.

А₁ – не вийде з ладу I.

А₂ – не вийде з ладу II.

А₃ – не вийде з ладу III.

1) Подія А – вийде з ладу тільки один елемент.

A = A₂ A₃ + A₁ A₃ + A₁ A₂

P(A) = q₁ p₂ p₃ + q₂ p₁ p₃ + p₁ p₂ q₃ = 0,131 0,769 0,719 + 0,231 0,869 0,719+

+0,869 0,769 0,281 = 0,0724 + 0,1443 + 0,1878 = 0,405

2) Подія B – вийде з ладу хоча б один елемент

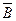– не вийде з ладу жодний елемент.

P(B) = 1 – P(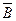) = 1- p₁ p₂ p₃ = 1 – 0,869 0,769 0,719 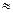0,52

Задача 6. В першій урні К білих і L чорних куль, а в другій М білих і N чорних куль. З першої урни навмання виймають Р куль, а з другої - Q куль. Знайти імовірність того, що серед вибраних куль:

1) Всі кулі одного кольору;

2) Лише три білих кулі;

3) Хоча б одна біла куля.

К = 7; L = 6; M = 4; N = 7; P = 3; Q = 2

I урна: 7 білих 6 чорних 3 к

II урна: 4 білих 7 чорних 2 к

1) Подія А – всі кулі одного кольору

2) Подія В – всі кулі білі

3) Подія С – всі кулі чорнi

B: n₁ = n₂ =

m₁ = m₂ =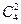

P(B) = = = = =

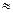= 0,013

C:n₁ = n₂ = m₁ = m₂ =

P(C) = = = = 0,027

P(A) = P(B) + P(C) = 0,13 + 0,27 = 0,4

Задача 7. В урні міститься К чорних і білих куль, до них додають L білих куль. Після цього з урни навмання виймають М куль. Знайти ймовірність тлго,що всі вибрані кулі є білими, припускаючи, що всі можливі варіанти (гіпотези) про початковий вміст урни є рівно можливими.

К = 6, L = 3, М = 5

6 білих і чорних куль + 3 білих кулі.

5 куль виймають.

А – вийняті 5 кульок – білі.

Сформулюємо гіпотези про початковий склад кульок:

Н₁ – 6 білих і 0 чорних куль

Н₂ – 5 білих і 1 чорна кулі

Н₃ – 4 білих і 2 чорних кулі

Н₄ – 3 білих і 3 чорних кулі

Н₅ – 2 білих і 4 чорних кулі

Н₆ – 1 білих і 5 чорних кулі

Н₇ – 0 білих і 6 чорних кулі

P(H₁) = P(H₂) = P(H₃)…… P(H₇) =

P_H1(A) = 1

P_H2(A) = = = =

P_H3(A) = = = =

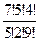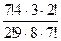P_H4(A) = = = =

P_H5(A) = = = =

P_H6(A) = 0 = P_H7(A)

За формулою повної імовірності:

P(A) = P(H₁) P_H1(A) + P(H₂ ) P_H2(A) + P(H₃) P_H3(A) + P(H₄) P_H4(A) +

+ P(H₅) P_H5(A) = = = =

= = , отже Р(А) =

Задача 8. В одній урні К білих і L чорних куль, а в другій М білих і N чорних куль. З першої урни навмання виймають Р куль, і перекладають в друга урну. Після цього з другої урни виймають R куль. Знайти ймовірність того, що всі кулі, які виймають з другої урни, є білими.

K = 7, L = 5, M = 2, N = 4, P = 3, R = 4

I урна: 7 білих і 5 чорних

3 кульки

II урна: 2 білих і 4 чорних 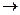виймають 4 кульки

А – вийняті 4 кулі є білими

Сформулюємо гіпотези щодо вийнятих 3 кульок з I урни:

H₁ – 3 білих і 0 чорних

H₂ – 2 білих і 1 чорна

H₃ - 1 біла і 2 чорних

H₄ - 0 білих і 3 чорних

Щоб можливо було вийняти 4 білі кулі з ІІ урни, необхідно, щоб виконалась гіпотеза Н₁ або Н₂

Р(H₁) = = = =

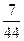
P(H₂) = = = =

P_H1(A) = = = =

P_H2(A) = = = =

P(H) = P_H1(A) P(H₁) + P(H₂) P_H2(A) = = = =

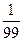
Задача 9. В піраміді стоять R гвинтівок, з них L з оптичним прицілом. Імовірність того, що стрілець, стріляючи із гвинтівки з оптичним прицілом, влучить у мішень дорівнює P. Імовірність того, що стрілець, стріляючи із гвинтівки без оптичного прицілу, влучить у мішень дорівнює P. Знайти, що стрілець влучить у мішень, стріляючи із навмання обранної гвинтівки.

K = 14; P₁ = 0,81; P₂ = 0,46 R = 19; L = 4

15 без приціла; 4 з прицілом.

А – стрілець влучить з гвинтівки, вибраної навмання.

Сформулюємо гіпотези щодо вибору гвинтівки

Н₁ – вибрано гвинтівку з оптичним прицілом.

Н₂ - вибрано гвинтівку без оптичного прицілу.

P(H₁) = 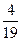P(H₂) =

P_H1(A) = 0,81 P_H2(A) = 0,46

P(A) = P(H₁) P_H1(A) + P(H₂) P_H2(A) = = =

= = =

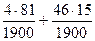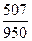
Задача 10. В монтажному цеху до пристрою приєднується електродвигун. Електродвигуни постачаються 3-ма заводами. На складі є електродвигуни цих заводів, відповідно в кількості М М М одиниць, які можуть безвідмовно працювати до кінця гарантійного терміну з імовірностями відповідно РРР. Робітник навмання обирає один електродвигун і монтує його до пристрою. Знайти ймовірність того, що змонтований електродвигун, який працює безвідмовно до кінця терміну, виготовлений на першому, другому, або третьому заводі.

K = 14; p₁ = 0,85; p₂ = 0,76; p₃ = 0,71; m₁ = 19; m₂ = 6; m₃ = 11

I II III

M 19 6 11

p 0,85 0,76 0,71

А – електродвигун працює безвідмовно.

Н₁ – цей двигун виготовлено на першому заводі.

Н₂ – цей двигун виготовлено на другому заводі.

Н₃ – цей двигун виготовлено на третьому заводі.

P(H₁) = P(H₂) = P(H₃) =

P_H1(A) = 0,85 P_H2(A) = 0,76 P_H3(A) = 0,71

P(A) = P(H₁) P_H1(A) + P(H₂) P_H2(A) + P(H₃) P_H3(A) = =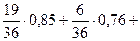

= = =

Імовірність того, що двигун виготовлено на першому заводі при умові, що він працює безвідмовно:

P_A(H₁) = = =

на другому:

P_A(H₂) = = = =

на третьому:

P_A(H₃) = = =

Дата добавления: 2015-10-23