Detronarea legii conservării energiei

Rezolvarea problemei energetice a fost pentru mine una din principalele preocupări. Un puternic imbold a constituit-o şi problema ecologică. Ştiinţa actuală nu numai că este incapabilă să rezolve aceste probleme stringente, dar interzice căutarea şi implementarea unor noi surse energetice ecologic pure. Citez: “ Legea conservării energiei interzice obţinerea de lucru în cantităţi mai mari decât cantitatea de energie consumată ” pag. 127[1]. Altfel spus, un obstacol în realizarea unor proiecte promiţătoare şi de viitor îl constituie rigiditatea mentalităţii fizicienilor, savanţilor noştri de azi, care au ridicat la rangul de dogmă nişte erori (legi de conservare) sigilându-le cu ştampila intangibilităţii.

“ La mijlocul sec. XIX numeroasele experienţe au demonstrat că energia mecanică nu dispare niciodată fără urmă. De exemplu, ciocanul cade pe o bucată de plumb – un sistem analogic cu ciocanul vom descrie în experimentele de mai jos (n. a.) – şi plumbul se încălzeşte într-un mod bine determinat. Forţele de frecare frânează corpurile, care în acest caz se încălzesc. Pe baza observărilor numeroase de acest fel şi generalizării datelor experimentale a fost formulată legea conservării energiei. Energia în natură nu apare din nimic şi nu dispare: cantitatea de energie este invariabilă, ea trece doar dintr-o formă în alta. Legea conservării energiei dirijează toate fenomenele naturii şi le reuneşte. Ea se respectă absolut: nu se ştie nici un caz, când ea nu s-ar respecta. Această lege a fost descoperită la mijlocul sec. XIX de savantul german R. Mayer (Maier, 1814-1878), medic de profesie, de savantul englez J. Joyle (Joul, 1818-1889), şi a fost formulată complet în lucrările savantului german H. Helmholtz (Helmholţ, 1821-1894)” pag. 63[2]

Pentru formularea unei legi fundamentale, absolute, nu s-au găsit experimente mai credibile? Chiar că-i lege din ciocan, ce a adus omenirea în pragul unui dezastru! Repet: “ Legea conservării energiei interzice obţinerea de lucru în cantităţi mai mari decât cantitatea de energie consumată ” pag. 127¹. Consider că o lege din fizică trebuie să aducă lămuriri şi în nici un caz să nu interzică!

Personal consider aberantă ideea de a conserva energia („ energhea ” – acţiune). Această afirmaţie o fac în baza unor îndelungate cercetări ştiinţifice în domeniul fizicii mecanice. Sunt ferm convins că legea conservării şi transformării energiei este falsă, ceea ce doresc să vă demonstrez şi Dvs. cu ajutorul unui experiment simplu şi anume: ridicăm la o înălţime oarecare o greutate în formă de bară, având la o extremă un punct de sprijin cu posibilitatea de a se roti în plan vertical, iar la cădere obţinem un lucru mai mare – un lucru echivalent cu lucrul efectuat de o greutate de 1,33 ori mai mare decât bara, ce cade de la aceeaşi înălţime (mai multe exemple puteţi găsi în publicaţiile [3] şi [4]).

Fizica este o ştiinţă experimentală. Aceasta înseamnă că legile fizicii se stabilesc şi se verifică acumulând şi comparând date experimentale. Formulele din fizică exprimă anumite relaţii care trebuie să existe între mărimile măsurate. Aşadar, rezultatul diferit al măsurărilor obţinute în cadrul aceluiaşi experiment ne conduce la concluzii absolut contrare. Diferenţa dintre valori de 30% este o mărime substanţială ce nu poate fi neglijată sau considerată o eroare a măsurărilor.

Pentru a înţelege mai bine aceste afirmaţii, vom analiza următorul fenomen. Acesta reprezintă un sistem format de o greutate sub formă de bară având la o extremă un punct de sprijin cu posibilitatea de a se roti în plan vertical. Vom calcula energia potenţială a barei în diferite puncte. Bara (fig. 1) cu lungimea l de 0,6 m şi cu masa m_b de 2 kg o împărţim în 12 părţi egale.

Folosind formula: calculăm forţa de greutate în cele 12 puncte ale barei. Unde: F este forţa de greutate ce acţionează în punctul cercetat (kgf), G – masa (greutatea) barei (kg), l – lungimea barei (m), x – distanţa de la axa de rotaţie până în punctul cercetat (m).

Vom obţine acelaşi rezultat, dacă în acest caz vom folosi dinamometrul pentru determinarea forţei de greutate în cele 12 puncte ale barei. Scriem datele obţinute în tabelă şi calculăm pentru fiecare punct cercetat ce se află la distanţa h energia potenţială a barei Wp în comparaţie cu punctul B (fig. 1).

Conform teoriei actuale avem: F₁ · l₁ = M₁ şi F₂ · l₂ = M₂

Se ştie că: F₁ < F₂ şi l₁ > l₂ (fig. 1)

Conform datelor din tabela 1 avem: M₁ = M₂ sau Wp = mgh = 5,88 J – constant.

Tabela 1

m	Forţa de greutate ce acţio­nează în punctul cercetat	kgf					2,4		1,7	1,5	1,4	1,2	1,1
g	Acceleraţia căderii libere	m/s^2	9,81 const.
h	Distanţa de la axa de rotaţie până în punctul cercetat	m	0,05	0,1	0,15	0,2	0,25	0,3	0,35	0,4	0,45	0,5	0,55	0,6
W	Energia potenţială a barei	J	5,88 const.

Se vede clar că energia potenţială Wp a barei (fig.1), calculată teoretic conform fizicii actuale, este o mărime constantă şi are aceeaşi valoare în toate punctele de pe bară (vezitabela 1). De aceea, indiferent de punctul de pe bară folosit în timpul experimentelor, vom obţine în rezultat aceeaşi energie potenţială (accentuez, conform „ teoriei ” actuale!). Pentru simplificarea acestor calcule în fizică a fost introdusă noţiunea “ centrul masei ”, deci calcularea energiei potenţiale Wp a unui corp rotativ (fig.1) în comparaţie cu un punct numit (de la A la B) nu necesită eforturi: Wp = mgh .

Dacă valorile m şi h sunt mărimi constante, atunci şi energia potenţială a corpului rămâne constantă în orice împrejurări (?!). Conducându-ne de legile din fizică obţinem: W₁ = W₂ sau W p.b.– constant (de la A la B). Doresc să menţionez unele afirmaţii ale fizicii actuale: „ Energia mecanică E a unui sistem izolat de corpuri se conservă ” pag. 87[5]. Iar „ Proprietatea de conservare este proprietatea de a rămâne invariabil ” pag. 102[6]. Sau „ Energia mecanică totală a unui sistem izolat de corpuri, care interacţionează prin forţe de gravitaţie sau forţe elastice, se menţine invariabilă la orice mişcări ale corpurilor din sistem ” pag. 120⁶. Consider că în acest caz ştiinţa actuală ne duce în eroare.

Personal nu sunt de acord cu această „ teorie ”, deoarece în urma verificării acestei „ teorii ” am constatat că nu coincide cu practica. În cazul experimentului propus avem un sistem închis, izolat, în care deplasarea aceluiaşi corp pe o distanţă egală ne permite să obţinem energii diferite (diferenţa dintre valori de 30%), ceea ce vine în contradicţie cu legea conservării şi transformării energiei. Marele savant rus M. V. Lomonosov spunea:

“ Un experiment eu îl pun mai presus decât o mie de păreri născute de imaginaţie ”

Cu ajutorul unei machete vom demonstra acest fenomen. Pentru efectuarea experimen­tului sunt necesare o serie de transformări a energiei, apoi comparăm valorile obţinute. Este evident că nu toate mărimile fizice pot fi determinate prin măsurări directe. Uneori suntem nevoiţi să recurgem la măsurări indirecte, de aceea în cazul dat vom folosi resortul. Factorii importanţi, care nu pot fi neglijaţi, constau în aceea că sistemul trebuie să fie echivalent în ambele variante, adică: nu se permite să schimbăm masa barei m_b (se are în vedere cantitatea de substanţă a barei), să mărim sau să micşorăm distanţa h (înălţimea la care se ridică greutatea – bara), iar arcul în poziţia iniţială nu trebuie să fie deformat.

Macheta reprezintă un sistem format de o greutate sub formă de bară având la o extremă un punct de sprijin cu posibilitatea de a se roti în plan vertical (fig. 2, 3 şi 4). Notăm poziţia iniţială a barei cu litera A, iar poziţia în care toată energia cinetică Wc a barei s-a transformat în energia potenţială Wp a arcului cu litera B. În poziţia A bara posedă o energie potenţială mai mare în comparaţie cu poziţia B. Menţionez că linia EE¢ este paralelă cu linia DD¢ şi paralelă cu linia OO¢ – EE¢ || DD¢ || OO¢.

Fig. 2 Fig. 3 Fig. 4

Lăsăm să cadă bara din punctul A până în punctul B (fig. 2). La cădere Wp a barei se transformă în Wc, apoi Wc se transformă în Wp (deformarea arcului). Cu alte cuvinte energia potenţială şi cinetică a barei se cheltuieşte pentru deformarea resortului (fig. 2).

Aceeaşi bară o lăsăm să cadă din punctul A (vezi fig. 3), dar schimbăm punctul de legătură cu bara. Prin urmare Wc se va cheltui pentru deformarea aceluiaşi arc. Se vede clar că bara a ajuns până în punctul C (fig. 3). Pentru claritate ne vom imagina că am redus cu mult viteza de cădere a barei, prin urmare observăm că bara aflându-se în punctul B (fig. 3) mai posedă o oarecare energie – D Wc. Datorită acestei energii D Wc bara se va deplasa din punctul B până în punctul C (fig. 3). Această energie cinetică D Wc trebuie s-o transformăm în energie potenţială D Wp cu condiţia să respectăm regulile prestabilite, şi anume: sistemul trebuie să fie echivalent în ambele variante, nu ni se permite să mărim distanţa BC (fig. 3). În acest caz (vezi figura 4) vom utiliza un arc suplimentar cu o rigiditate (k₃) mai mică. Pentru a evita erorile repetăm experimentul din figura 2 şi din figura 4, apoi comparăm rezultatele obţinute.

Notăm:

Wp – energia potenţială,

Wc – energia cinetică,

Wp₁ – energia potenţială pe care o posedă bara până la transformare, prima variantă,

Wp₂ – energia potenţială pe care o posedă bara până la transformare, varianta a doua,

Wp.t.₁ – energia potenţială după transformare, prima variantă (fig. 2),

Wp.t.₂ – energia potenţială după transformare, varianta a doua (fig. 4),

D Wc – energia cinetică mică în comparaţie cu energia cinetică exercitată în sistem,

D Wp – energia potenţială mică în comparaţie cu energia potenţială exercitată în sistem,

e_x – pierderile de energie din sistem (fig. 2 şi fig. 4).

Notăm prin Wx – valoarea energiei cinetice [pag. 118, tab. 1][7] a unui punct (x) cercetat al corpului rotativ în sistemul dat (fig. 2 şi fig. 4).

(1)

Unde: m_x, l_x şi w_x – sunt mărimi ce corespund fiecărui punct (x) cercetat de pe bară.

e_x – pierderile de energie din sistem.

Pentru fiecare sistem în parte putem scrie următoarele relaţii:

pentru figura 2 (2)

pentru figura 4 (3)

Legea conservării şi transformării energiei mecanice totale ne spune că: „ Energia nu se creează şi nici nu dispare, doar se transmite de la un corp la altul, ori se transformă dintr-o formă în altă formă în aceeaşi cantitate” pag. 102[8]. Conform acestei legi avem:

pentru figura 2 (4)

pentru figura 4 (5)

„La rezolvarea problemelor în mecanică conform legii conservării energiei se permite de a nu lua în consideraţie starea intermediară prin care trece sistemul, dar se va compara starea iniţială cu cea finală. De aceea la rezolvarea problemelor în mecanică trebuie de clarificat dacă se poate aplica legea conservării şi transformării energiei la problema dată – aceasta contribuie la o rezolvare simplă şi rapidă” pag. 102⁸. Deoarece schimbarea energiei potenţiale a sistemului nu depinde de starea intermediară putem scrie relaţiile:

pentru figura 2 (6)

pentru figura 4 (7)

Deoarece: m₁ = m₂ g – const. h₁ = h₂ obţinem: sau Wp₁ = Wp₂

Conform legii conservării energiei dacă: Wp₁ = Wp₂ sau (8)

Atunci trebuie şi: Wp.t.₁ = Wp.t .₂ sau e₁ = + e₂ (9)

Deoarece: k ₁ = k ₂ şi x ₁ = x ₂ atunci şi (10)

În urma reducerii relaţiei 9 în baza relaţiei 10 obţinem: e₁ = + e₂ (11)

Unde: e₁ = e^′₁ + e^″₁ + e^′′′₁ iar: e₂ = e^′₂ + e^′′₂ + e^′′′₂ + e₃

e^′₁ şi e^′₂ – pierderile de energie în rulmenţi,

e^′′₁, e^′′₂ şi e₃ – pierderile de energie la deformarea arcului,

e^′′′₁ şi e^′′′₂ – pierderile de energie la rezistenţa aerului (diferenţa dintre

valori – e^′′′₁ şi e^′′′ ₂ – este foarte mică, dar totuşi există).

După o analiză atentă, ştiinţifică, multilaterală, bazată pe valorile reale ale experimentului

s-a constatat că:

e^′₁ < e^′₂ deoarece F₁ < F₂ (vezi fig. 2 şi fig. 4)

e^′′₁ < e^′′₂ + e₃ deoarece e^′′₁ = e^′′₂ (vezi relaţia 10)

e^′′′₁ > e^′′′₂ deoarece w₁ > w₂ (măsurări directe).

În realitate obţinem: e₁ < e₂ sau e ^′₁ + e^′′₁ + e^′′′₁ < e^′₂ + e^′′₂ + e^′′′₂ + e₃ (12)

Unde: e₂ - e₁ = e₄ (13)

În urma reducerii relaţiei 11 în baza relaţiei 12 obţinem: 0 = + e₄ (14)

Relaţia 14 vine în contradicţie cu legea conservării energiei mecanice totale care ne spune că: în cazul oricărei transformări de energie dintr-o formă în altă formă se păstrează egalitatea. Conform acestei legi, partea stângă a relaţiei 14 trebuie să fie egală cu partea dreaptă a relaţiei 14, însă, în realitate nu obţinem o egalitate.

Deci, până la transformare am avut o egalitate: Wp₁ = Wp₂ sau (15)

După transformare am obţinut o inegalitate: Wp.t.₁ ¹ Wp.t.₂ sau Wp.t.₁ < Wp.t.₂ (16)

În realitate relaţia: nu se respectă, am obţinut: (17)

Deci, după transformare am obţinut: 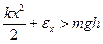(apare un surplus de energie) (18)

ceea ce vine în contradicţie cu legea conservării şi transformării energiei mecanice totale.

Conform acestei legi dacă: Wp₁ = Wp₂ atunci trebuie şi Wp.t.₁ = Wp.t.₂ (19)

ceea ce în cazul dat nu se respectă, experimental am obţinut: Wp.t.₁ < Wp.t.₂ (20)

Energia potenţială a barei nu poate fi calculată utilizând formula cunoscută Wp = mgh. Energia potenţială a corpului depinde nu numai de poziţia lui în comparaţie cu alt corp, dar şi de modalitatea interacţiunii dintre aceste corpuri. Fiecărui punct al corpului rotativ îi co­respunde energia potenţială respectivă. Deci, e evident că e necesară o lege nouă pentru a explica acest fenomen. Această lege poate fi formulată astfel: energia cinetică a corpului în formă de bară, care se roteşte pe o axă orizontală ce trece prin capătul barei perpendicular pe ea, variază invers proporţional în raport cu lungimea braţului.

Fizicienii conservatori neagă cu vehemenţă justeţea acestei teorii, argumentând că diferenţă de energie nu există – totul se află într-un echilibru total conform legii conservării şi transformării energiei. Ei spun că energia dispărută (lipsă) se află sub formă de energie termică a resortului (fig. 2), cu toate că în cadrul experimentului (fig. 4) se observă şi un surplus de energie (apare). În acest caz sunt nevoit să demonstrez acelaşi experiment utilizând altă metodă de măsurare a energiei.

Repet, calcularea energiei necesare pentru efectuarea acestui lucru (deformarea resortului din fig. 2 şi fig. 4) conform formulelor existente – mgh – nu este corectă. De aceea am hotărât să măsor această energie indirect, prin deformarea unei plăcuţe din aluminiu, conform testării metalelor la duritate după metoda lui Brinella. Plăcuţa va fi amplasată în trei puncte diferite (vezi figurile 5, 6 şi 7). În acest experiment vom utiliza o bară cu lungimea de 0,52 m şi cu masa de 3 kg (fig. 5, 6, 7). Notăm poziţia iniţială (orizontală) a barei cu litera A, iar cu litera B – poziţia barei deplasată în sus cu 90⁰ (verticală).

Fig. 5 Fig. 6 Fig. 7

Ridicăm bara din punctul A până în punctul B (fig. 5). Noi am efectuat un lucru oarecare A ₁. Instalăm plăcuţa de aluminiu în partea extremă a punctului de sprijin (fig. 5). Lăsăm bara să cadă din punctul B până în punctul A. În acest caz se va efectua un lucru A ₂ de deformare a plăcuţei de aluminiu (fig. 5).

Repetăm ridicarea barei din punctul A până în punctul B (fig. 6). Noi am efectuat un lucru A ₃. Instalăm plăcuţă de aluminiu la centru (fig. 6). Lăsăm bara să cadă din punctul B până în punctul A. În acest caz se va efectua un lucru A ₄ de deformare ale aceleiaşi plăcuţe de aluminiu (fig. 6).

Mai ridicăm o dată bara din punctul A până în punctul B (fig. 7). Noi am efectuat un lucru A ₅. Instalăm plăcuţă de aluminiu cât mai aproape de punctul de sprijin al barei (figura 7). Lăsăm bara să cadă din punctul B până în punctul A. În acest caz se va efectua un lucru A ₆ de deformare ale aceleiaşi plăcuţe de aluminiu (fig. 7).

Să analizăm minuţios acest experiment.

Avem: A ₁, A ₃ şi A ₅ – lucrul efectuat la ridicarea barei în toate cele trei cazuri.

Unde: A ₁ = A ₃ = A ₅ – deoarece greutatea barei m _b şi înălţimea h sunt mărimi neschimbătoare (m _b şi h – constante), iar bara o vom ridica în toate cele trei cazuri din acelaşi punct – capătul opus punctului de sprijin (condiţie obligatorie).

Conform experimentului avem: A ₁ = A ₃ = A ₅ unde: A ₁ = W ₁ + ε₁

A ₃ = W ₃ + ε₃

A ₅ = W ₅ + ε₅

W₁, W₃ şi W₅ – energia cheltuită pentru ridicarea barei în toate cele trei cazuri (fig. 5, 6, 7)

ε₁, ε₃, şi ε₅ – pierderile de energie la ridicarea barei (în rulmenţi şi la rezistenţa aerului).

Am obţinut: A ₂, A ₄ şi A ₆ – lucrul efectuat la deformarea plăcuţei din aluminiu în toate cele trei cazuri. La căderea barei, conform experimentului, lucrul efectuat la deformarea plăcuţei din aluminiu în fiecare caz a fost diferit: A ₂ ≠ A ₄ ≠ A ₆.

Prin urmare constatăm că şi energia W₂, W₄, şi W₆ necesară pentru deformarea plăcuţei din aluminiu în toate cele trei cazuri este diferită: W ₂ ≠ W ₄ ≠ W ₆.

Comparând lucrul efectuat la deformarea plăcuţei din aluminiu în toate cele trei cazuri, vom avea:

A ₂ < A ₄ < A ₆ sau W ₂ < W ₄ < W ₆

unde: A ₂ = W ₂ + ε₂ + ε^'₂ A ₄ = W ₄ + ε₄ + ε^'₄ A ₆ = W ₆ + ε₆ + ε^'₆

ε₂, ε₄ şi ε₆ – pierderile de energie la căderea barei (în rulmenţi şi la rezistenţa aerului),

ε^'₂, ε^'₄ şi ε^'₆ – pierderile de energie la deformarea plăcuţei din aluminiu.

Conform experimentului vedem că la ridicarea barei în toate cele trei cazuri a fost efectuat acelaşi lucru:

A ₁ = A ₃ = A ₅ sau W ₁ = W ₃ = W ₅

Iar la căderea barei lucrul efectuat la deformarea plăcuţei din aluminiu în toate cele trei cazuri a fost diferit:

A ₂ < A ₄ < A ₆ sau W ₂ < W ₄ < W ₆

Făcând o analiză aprofundată a acestui experiment vedem că ştiinţa actuală ne duce în eroare, afirmând despre legea conservării energiei că: „ Ea se respectă absolut: nu se ştie nici un caz, când ea nu s-ar respecta ” pag. 63[9]. În cazul experimentului propus avem: un sistem închis, izolat, în care deplasarea aceluiaşi corp pe o distanţă egală ne permite să obţinem energii diferite, ceea ce vine în contradicţie cu legea conservării energiei.

Conform experimentului, am avut: A ₁ = A ₃ = A ₅ sau W₁ = W₃ = W₅

am obţinut: A ₂ < A ₄ < A ₆ sau W ₂ < W ₄ < W ₆

Menţionez că:

I v. – W ₁ + ε₁ > W ₂ + ε₂ + ε^'₂ nu se respectă legea conservării energiei (dispare) (fig. 5)

II v. – W ₃ + ε₃ = W ₄ + ε₄ + ε^'₄ se respectă legea conservării energiei (fig. 6)

III v. – W ₅ + ε₅ < W ₆ + ε₆ + ε^'₆ nu se respectă legea conservării energiei (apare) (fig. 7).

Argumentez: în prima variantă lucrul A₂ a fost efectuat de → = 1,5 kgf (fig. 5)

în varianta a doua lucrul A₄ a fost efectuat de → m_b = 3 kgf (fig. 6)

în varianta a treia lucrul A₆ a fost efectuat de → 1,33m_b = 4 kgf (fig. 7)

unde: m_b – masa barei (kgf).

O analiză ştiinţifică atentă ne spune că anume acest surplus de greutate (4kgf) duce la obţinerea unui lucru mai mare. Cu toate că bara cu masa de 3 kg în cadrul experimentului, rămâne constantă în toate cele trei cazuri. Ţin să menţionez că acest surplus virtual de greutate (1,33m_b = 4 kgf) este obţinut datorită punctului de sprijin (vezi fig. 7).

Pentru verificarea acestei teorii vom efectua un experiment suplimentar în care vom utiliza greutăţi cu mărimi identice experimentului anterior:

m₁ = 1,5 kg, m₂ = 3 kg, m₃ = 4 kg.

Cunoaştem cu toţii noţiunea „ centrul masei ”. În experimentul anterior am folosit o greutate cu masa de 3 kg în formă de bară cu lungimea de 0,52 m. Prin urmare centrul masei al acestei greutăţi este la distanţa de 0,26 m, de aceea vom ridica greutăţile cu masa de 1,5 kg, 3 kg şi 4 kg la înălţimea de 0,26 m (vezi figurile 8, 9 şi 10).

Fig. 8 Fig. 9 Fig. 10

Ridicăm greutatea m₁ (1,5 kg) la înălţimea h₁ (0,26 m). Noi am efectuat un lucru A₇ (fig. 8). Lăsăm să cadă această greutate pentru a efectua un lucru A₈ de deformare a plăcuţei din aluminiu.

Apoi ridicăm greutatea m₂ (3 kg) la înălţimea h₂ (0,26 m). În acest caz noi vom efectua un lucru A₉ (fig. 9). Lăsăm să cadă şi această greutate pentru a efectua un lucru A₁₀ de deformare a aceleiaşi plăcuţe din aluminiu.

Ridicăm şi greutatea m₃ (4 kg) la înălţimea h₃ (0,26 m). În acest caz noi vom efectua un lucru A₁₁ (fig. 10). Lăsăm să cadă şi această greutate pentru a efectua un lucru A₁₂ de deformare a aceleiaşi plăcuţe din aluminiu.

Să analizăm minuţios şi acest experiment. Conform experimentului avem:

1. A ₇ < A ₉< A ₁₁ deci şi W ₇ < W ₉ < W ₁₁ (fig. 8, fig. 9 şi fig. 10)

W ₇, W ₉ şi W ₁₁ – energia cheltuită la ridicarea greutăţilor (1,5 kg, 3 kg şi 4 kg).

W₇ = m₁gh₁ = 1,5 · 9,81 · 0,26 = 3,8259 J,

W₉ = m₂gh₂ = 3 · 9,81 · 0,26 = 7,6518 J,

W₁₁ = m₃gh₃ = 4 · 9,81 · 0,26 = 10,2024 J,

2. A ₈ < A ₁₀< A ₁₂ deci şi W ₈ < W ₁₀ < W ₁₂ (fig. 8, fig. 9 şi fig. 10)

W ₈, W ₁₀ şi W ₁₂ – energia cheltuită pentru deformarea plăcuţelor din aluminiu.

W ₈ < W ₁₀ < W ₁₂ deoarece m₁ < m₂ < m₃ iar h₁ = h₂ = h₃

Să comparăm mărimea lucrului efectuat în experimentul anterior (fig. 5, fig. 6 şi fig. 7) cu mărimea lucrului efectuat în experimentul dat (fig. 8, fig. 9 şi fig. 10).

În realitate, prin măsurări directe, obţinem: A ₂ = A ₈ (fig. 5 şi fig. 8)

A ₄ = A ₁₀ (fig. 6 şi fig. 9)

A ₆ = A ₁₂ (fig. 7 şi fig. 10)

Conform experimentului avem: A₆ = A₁₂ deci şi W₆ = W₁₂

W ₆ şi W ₁₂ – energia necesară pentru lucrul efectuat la deformarea plăcuţei din aluminiu.

Menţionez că: lucrul A₆ a fost efectuat de o greutate cu masa de 3 kg în formă de bară cu lungimea de 0,52 m având centrul masei la distanţa de 0,26 m, adică ridicată la înălţimea de 0,26 m (fig. 7), iar lucrul A₁₂ a fost efectuat de o greutate cu masa de 4 kg ridicată tot la înălţimea de 0,26 m (fig. 10).

În cadrul experimentului am ridicat o greutate cu masa de 3 kg la înălţimea de 0,26 m, iar la cădere am obţinut un lucru echivalent cu lucrul efectuat de o greutate cu masa de 4 kg ridicată la aceeaşi înălţime (0,26 m) – ceea ce am intenţionat să demonstrez.

În baza celor demonstrate vedem că de la acelaşi corp m _b (figurile 2, 4, 5, 6 şi 7) ce cade de la o înălţime h constantă, obţinem valori diferite a lucrului efectuat (A ₂ < A ₄ < A ₆) deci şi valori diferite a energiei (W ₂ < W ₄ < W ₆) – conform noii legi formulate.

Aceste experimente ne demonstrează că energiaNUSECONSERVĂ, prin urmare energia NU este materie. Energia este o MĂRIME FIZICĂ ce caracterizează un lucru. Cu alte cuvinte energia este măsura mişcării materiei. Conform acestor experimente declar cu fermitate că legea conservării energiei este incorectă. De aceea legea conservării şi transformării energiei NU poate fi un obstacol în realizarea unor proiecte promiţătoare şi de viitor – perpetuum mobile (am descoperit secretul mecanismului salvator).

Personal consider că numai materia se conservă, adică nu variază (nu dispare şi nu apare din nimic). În toată programa cursurilor de fizică nu va fi găsită formularea legii conservă­rii şi transformării materiei, de aceea consider necesar de formulat această lege: materia (substanţa) nu se creează din nimic şi nu dispare fără urmă, doar în urma unui proces trece dintr-o stare de agregare în altă stare, în aceeaşi cantitate. Consider că această lege este baza învăţăturii despre fizică. În Univers nu există nimic altceva decât materie (să nu se confunde stările de agregare ale materiei). Or, fizica se ocupă cu studierea tuturor formelor de mişcare şi transformare a materiei, inclusiv toate stările de agregare.

Până în prezent (2013) sunt cunoscute doar patru stări de agregare a materiei. Consider că în natură există mai multe stări de agregare a materiei decât cele 4 cunoscute. Presupun vreo 9 stări de agregare, mai corect ar fi grupe – sunt de părerea că materia trebuie să fie divizată pe grupe – deoarece într-o grupă poate să fie un număr infinit de substanţe asemănătoare. O dovadă de necontestat este următoarea definiţie: „ Formă de existenţă a materiei care se manifestă prin acţiunea asupra acului magnetic se numeşte câmp magnetic ” pag. 87[10]. Sau: „ Ca şi celelalte tipuri de câmpuri cunoscute – câmp gravitaţional, câmp electric şi câmp magnetic – câmpul electromagnetic este o formă de existenţă a materiei şi se observă prin acţiunea sa asupra corpurilor ” pag. 104[11]. Afirm cu certitudine că la acest capitol este necesar de făcut unele corectări şi completări.

Ion GABAREV inventator, cercetător ştiinţific (autodidact)

htth://gabarev.wordpress.com/ Tel: [phone]

[1] I. K. Kikoin, A. K. Kikoin, FIZICA, Manual pentru clasa 9 a şcolii medii, Chişinău “Lumina” 1991.

[2] G. I. Miakişev, B. B. Buhovţev, FIZICA, Manual pentru clasa a X-a a şcolii medii, Ediţia a II-a, “Lumina” Chişinău – 1995.

[3] Ion Gabarev, LIMITA POSIBILULUI?..., Studiu ştiinţific, Tipografia Centrală, Chişinău, 2006.

[4] Ion Gabarev, FIZICA COMPLEXĂ, Studiu ştiinţific, Tipografia Centrală, Chişinău, 2007.

[5] I. Botgros, V. Bocancea, N. Constantinov, FIZICĂ, Manual pentru clasa a VII-a.

[6] I. K. Kikoin, A. K. Kikoin, FIZICA, Manual pentru clasa 9 a şcolii medii, Chişinău “Lumina” 1991.

[7] А. Сибирский, Лукрэрь де лаборатор ла физикэ, пентру класа 8, Курс факултатив, Кишинэу “Лумина” 1979.

[8] Н.Н. Ефграфова, В.Л. Каган, Курс физики, Москва “Высшая школа” 1984.

[9] G. I. Miakişev, B. B. Buhovţev, FIZICA, Manual pentru clasa a X-a a şcolii medii, Ediţia a II-a, “Lumina” Chişinău – 1995.

[10] I. Botgros, V. Bocancea, N. Constantinov, FIZICĂ, Manual pentru clasa a VIII-a – Ed. 1. Cartier, 2003, Ministerul Educaţiei al Republicii Moldova.

[11] Tatiana Iacubiţchi, Anatol Sîrghi, FIZICĂ, Manual pentru clasa a IX-a, Litera, 2003, Ministerul Educaţiei al Republicii Moldova.

Дата добавления: 2015-10-23