Практично усі кристалічні діелектрики оптично анізотропні: електрична поляризованість Р кристала залежить від напрямку і вона визначається електричною анізотропією (симетрією) молекул та сил взаємодії між ними (анізотропія кристалічного поля). Розповсюдження хвиль у цих кристалах як і в інших прозорих речовинах визначається інтерференцією первинної та вторинних хвиль, що випромінюються молекулами. Тільки кристали кубічної симетрії є ізотропними.
В оптично анізотропних кристалах спостерігається явище подвійного променезаломлення, яке полягає в тому, що падаючий промінь світла породжує два промені: звичайний (о) та незвичайний (е) (див.Мал.167). Перший описується звичайним законом заломлення світла, а для другого закон заломлення не виконується тому, що відношення синусів кута падіння та кута заломлення залежить від кута падіння і не є сталою величиною.
Звичайний промінь лежить у площині падіння світла ¾ площині утвореній нормаллю до поверхні кристала та напрямком падаючого променя. Не звичайний промінь, навіть при нормальному падінні світла, не лежить у площині падіння.
Оптична вісь кристала ¾ напрямок у кристалі, вздовж якого падаючий промінь породжує лише собі подібний без подвійного променезаломлення ¾ звичайний та незвичайний промені не розділяються й мають однакові швидкості поширення.
Кристали можуть мати одну вісь (одноосьовий кристал) та дві осі (двоосьовий кристал).
Головна оптична площина (головний переріз) одноосьового кристалу для деякого променя ¾ площина, утворена цим променем та оптичною віссю кристала.
Звичайна хвиля лінійно поляризована в площині ^ головному перерізу і задовольняє закону Снеліуса. Незвичайна хвиля лінійно поляризована в площині головного перерізу.
У двовісному кристалі обидва заломлених променя поводяться як незвичайні.
Якщо у середині кристала уявно ввімкнути на мить джерело світла, то утворяться звичайний і незвичайний промені. Через одиницю часу вектори переміщення світла співпадуть із векторами швидкості і їх кінці утворять 
деякі поверхні, що називаються променевими, або індикатрисами швидкості.
Одна з цих поверхонь в одноосьовому кристалі є сфера, а друга ¾ еліпсоїд обертання, які дотикаються. Пряма ОО', проведена через точки дотику є оптична вісь кристала. Сфера відповідає звичайному променю, а еліпсоїд ¾ незвичайному. Променеві швидкості Vo і Ve обернено пропорційні їх показникам заломлення no, ne. Тому при Vo < Ve (no> ne) сфера вписана в еліпсоїд ¾ кристал називається оптично позитивним (" + ") (див.Мал.168), наприклад, кварц, кіноварь, каломіль, а при Vo > Ve (no< ne) еліпсоїд уписаний у сферу ¾ кристал називається оптично негативним (" - ") (див.Мал.169), наприклад, турмалін, ісландський шпат, апатит. У випадку двовісних кристалів обидві поверхні є еліпсоїдами, які можуть мати точки дотику.
Явище дихроїзму. Явище дихроїзму полягає у тому, що у деяких кристалах звичайні та незвичайні хвилі мають різні коефіцієнти поглинання. Наприклад, у кристалі турмаліну сильно згасає звичайна хвиля і при певній товщині кристала на виході з нього актуальною залишиться лише одна плоскополяризована незвичайна хвиля, тобто цей кристал можна застосовувати як поляризатор чи аналізатор. Поляризатори, виконані на основі дихроїзму, що мають невелику товщину ¾ плівки, називають поляроїдами.
16.4. Призма Ніколя
Призма Ніколя -є призма, вирізана з ісландського шпату 
¾ одноосьового, оптично негативного кристалу з no = 1.658 i ne = 1.486. Оптична вісь ОО' складає з нижньою гранню кут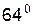 
( див.Мал.170 ). Призмарозрізана по діагональній площині SS' і склеєна канадським бальзамом з nкб = 1.550. Промінь, що падає нормально на бічну грань, породжує звичайну та незвичайну хвилі, які, не заломлюючись, приходять до границі розділу канадським бальзамом. Кут падіння звичайного променя на границю вибрано трошки більшим, ніж кут 
повного внутрішнього віддзеркалення
, а тому звичайний промінь повністю відбивається від канадського бальзаму. Незвичайний промінь вільно проходить через призму, залишаючись лінійно поляризованим у площині перпендикулярній головному перерізу.
16.5. Штучне подвійне променезаломлення
В ізотропних середовищах можна створити подвійне променезаломленняпри односторонньому стисненні кристалів кубічної симетрії, при накладанні електричного поля на рідини, аморфні тіла, гази (ефект Керра) та накладанні магнітного поля на рідини, скло, колоїди. При цьому подвійне променезаломлення характеризується різницею показників заломлення для звичайної та незвичайної хвиль
(1)
- для стиснення (s¾ нормальна напруга сили),
(2)
- для ефекту Керра (Е ¾ напруженість електричного поля),
(3)
- для магнітного поля (Н ¾ напруженість магнітного поля). Слід зазначити, що інерційність ефекту Керра складає 
і він може бути застосований як швидкодіючий затвор для світла, що проходить через два схрещених ніколя.
-
16.6. Оптично активні середовища
Оптично активними називаються середовища, які обертають площину поляризації лінійно поляризованого світла. До них відносяться розчин цукру, винна кислота, скипидар, кварц і т.п. Кут повороту визначається формулою
, (1)
де a ¾ стала обертання, L ¾ товщина шару активної речовини, який пройшло світло. Для оптично активних рідин 
, (2)
де C ¾ концентрація розчину, 
¾ густина розчину, 
¾ стала обертання розчину.
Ефект Фарадея ¾ виникнення оптичної активності в неактивних середовищах під впливом магнітного поля, із кутом повороту
j = VHL, (3)
де V ¾ стала Верде, H ¾ напруженість магнітного поля, L ¾ довжина шляху в речовині. Напрямок осі обертання площини поляризації співпадає або протилежний напрямкові напруженості Н, причому кут повороту в обох випадках однаковий, на відміну від природно оптично активних середовищ (див.Мал.39).
 |
16.7. Контрольні питання
1. Сформулюйте умови часової та просторової когерентності електромагнітних хвиль.
2. Одержіть умови max та min інтерференції у досліді Юнга.
3. Розрахувати багато променеву інтерференцію N когерентних електромагнітних хвиль при послідовному зсуві по фазі Dj у них.
4. Розрахуйте дифракційну картину Френеля на круглому отворі.
5. Розрахуйте дифракційну картину Френеля на дискові.
6. Розрахуйте дифракційну картину Фраунгофера на щілині: умови max та min.
7. Розрахуйте дифракційну картину Фраунгофера на дифракційній решітці; умови max та min.
8. Розрахуйте дисперсію дифракційної решітки.
9. Розрахуйте розрізнювальну здатність дифракційної решітки.
10. Розрахуйте дифракцію рентгенівського випромінювання на кристалічній решітцi.
11. Розрахуйте вираз для показника заломлення в дисперсному середовищі на основі класичної електронної теорії дисперсії.
12. Розрахуйте групова швидкість на прикладі розповсюдження двох близьких за частотами електромагнітних хвиль.
13. Одержіть вираз для інтенсивності світла в поглинанаючому середовищі.
14. Сформулюйте поняття лінійної, еліптичної та природної поляризації світла.
15. Сформулюйте поняття поляризатора та аналізатора світла та одержіть вираз для закону Малюса.
16. Дайте визначення кута Брюстера.
17. У чому полягає явище оптичної анізотропії одновісних кристалів?
18. Опишіть індикатриси швидкості та показника заломлення додатнього та від'ємного одновісного кристала.
19. Овишіть явище природного та штучного дихроїзму.
20. Опишіть та намалюйте принципову схему призми Ніколя.
21. Що являє собою природна та штучна оптична активність речовини? Наведіть приклади.
22. У чому полягає ефект Фарадея?
Дата добавления: 2015-10-29; просмотров: 161 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Reporting to parents | | | SMITH OF WOOTTON MAJOR |